Das Feld in der Energie-Theorie

Diese Beweislage in der IT hat uns ermutigt, die gleiche Problematik in der ET anzupacken und die Eigenschaften des Elementarteilchens in einem punktförmigen Koordinatensystem zu durchleuchten. Aus Symetriegründen zur IT werden wir deren Beschreibungen unter der minimalen Änderungen in diesem Kapitel nachempfinden. Wir werden den Vierergradient viermal auf das Viererpotential^7.1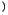$^)$ (5.2) anwenden. Anschließend werden wir die so entstandene Differentialgleichungen vierter Ordnung (die Viererdichte) über die Vierervolumen integrieren, um die Erhaltung des Viererpotentials nachzuweisen.

$$\fbox {$\rule[-4mm]{0cm}{1cm}i\displaystyle\int \limits_\Omega (\... ...k}\ . \ (\partial^{kj}\ . \ a^{kj})) \ d\omega_k^1 \ = \ (4\pi) \ a^{k1} \ \ $}$$ (7.1)

-i vor dem Integral ist als Kompensation zu dem imaginären Vierervolumenelement hinzugefügt.