




Nächste Seite: Der elektromagnetische Viererimpuls der
Aufwärts: Das positive, negative und
Vorherige Seite: Das positive, negative und
Inhalt
Index
Das skalare und Vektorpotential bilden in der dualen Physik die Komponenten
des Viererpotentials . In der IT ist
diese Beziehung für die Entfernungen 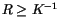 gleich:
gleich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_j \ = \ ( \ i\phi^- \ , \ \ \displ...
...\displaystyle\frac {As}{m} \ \quad \mbox{\bf Das Viererpotential der IT} \ \ $}$](IMG337.GIF) |
|
|
(5.1) |
Seine skalare Komponente ist das imaginäre Potential einer imaginären Ladung
aus der ET
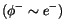 .
Dagegen ist seiner Vektorkomponente das magnetische Potential einer reeller
Ladung
aus der IT
.
Dagegen ist seiner Vektorkomponente das magnetische Potential einer reeller
Ladung
aus der IT
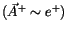 .
Die Dimension dieses Vierervektors wird mit
.
Die Dimension dieses Vierervektors wird mit
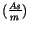 festgelegt.
Analog zu der IT können wir das Viererpotential der Energietheorie
für die Entfernungen
festgelegt.
Analog zu der IT können wir das Viererpotential der Energietheorie
für die Entfernungen
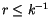 angeben:
angeben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}a^j \ = \ ( \ \displaystyle\frac {\v...
... \displaystyle\frac {Vs}{m} \ \quad \mbox{\bf Das Viererpotential de ET} \ \ $}$](IMG341.GIF) |
|
|
(5.2) |
Erwähnenswert ist seine skalare Komponente, mit der imaginären Ladung der
IT, die einen reellen Skalar der Energietheorie
(
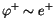 ) darstellt.
Seine imaginäre Komponente stellt die Bewegung einer reellen Ladung der ET
dar und
ist ein imaginärer Vektor
der ET (
) darstellt.
Seine imaginäre Komponente stellt die Bewegung einer reellen Ladung der ET
dar und
ist ein imaginärer Vektor
der ET (
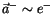 ). Das Viererpotential der ET weist eine andere
Dimension auf, die mit
). Das Viererpotential der ET weist eine andere
Dimension auf, die mit
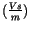 bezeichnet wird.
Die elektromagnetische Wechselwirkung in einem Atom lassen sich durch
das duale komplexe Viererpotential bis auf das Vorzeichen des Elementarteilchens
ermitteln. Der Atomkern ist ein komplexes Mehrteilchen-System, daß aus
Hadronen besteht. Die Erfahrung zeigt, daß die Hadronen eine
Multiteilchen-Struktur aufweisen, die man heute als eine Familie ansieht.
Für den Atomkern können wir sagen:
Befindet sich ein ET-Teilchen innerhalb der IT-Grenzen (im Kernbreich)
bezeichnet wird.
Die elektromagnetische Wechselwirkung in einem Atom lassen sich durch
das duale komplexe Viererpotential bis auf das Vorzeichen des Elementarteilchens
ermitteln. Der Atomkern ist ein komplexes Mehrteilchen-System, daß aus
Hadronen besteht. Die Erfahrung zeigt, daß die Hadronen eine
Multiteilchen-Struktur aufweisen, die man heute als eine Familie ansieht.
Für den Atomkern können wir sagen:
Befindet sich ein ET-Teilchen innerhalb der IT-Grenzen (im Kernbreich)
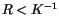 , so wird es als ein Teilchen im Medium Materie
(im Gegensatz zu Vakuum5.1
, so wird es als ein Teilchen im Medium Materie
(im Gegensatz zu Vakuum5.1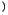 ) angesehen. Der Widerstand
(die Impendanz) dieses Mediums ist maßgebend für die elektromagnetische
Wechselwirkung im Kernbereich, die als starke Wechselwirkung bezeichnet
wird.
Für den Kernbereich eines Proton-Neutronen-Systems findet ebenfalls
das duale Viererpotential Verwendung. Im
Grenzgebiet (
) angesehen. Der Widerstand
(die Impendanz) dieses Mediums ist maßgebend für die elektromagnetische
Wechselwirkung im Kernbereich, die als starke Wechselwirkung bezeichnet
wird.
Für den Kernbereich eines Proton-Neutronen-Systems findet ebenfalls
das duale Viererpotential Verwendung. Im
Grenzgebiet (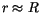 ) oder in der Kernoberfläche (die neutrale Zone) können
sich unter Umständen neutrale Teilchen
( Neutronen) einnisten.
Für die Impulstheorie schreiben wir:
) oder in der Kernoberfläche (die neutrale Zone) können
sich unter Umständen neutrale Teilchen
( Neutronen) einnisten.
Für die Impulstheorie schreiben wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\widehat{A}_j \ = \ ( \ i\widehat{\p...
...\ \displaystyle\frac {Vs}{m} \ \ \mbox{\bf Das Viererkernpotential der IT} \ $}$](IMG346.GIF) |
|
|
(5.3) |
Das Viererkernpotential der Energietheorie lautet:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\widehat{a}^j \ = \ ( \ \displaystyl...
...\ \displaystyle\frac {As}{m} \ \ \mbox{\bf Das Viererkernpotential der ET} \ $}$](IMG347.GIF) |
|
|
(5.4) |
Diese Gleichungen sind das duale Viererkernpotential.
In den Formeln (5.2) und (5.3) oder (5.4) sind einige äußerst wichtige Konstanten eingegangen :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varepsilon_0 \ = \ \mbox{die elektrische Feldkonstante oder {\bf Influenzkonstante}}\index{Influenzkonstante} \ $}$](IMG348.GIF) |
|
|
(5.5) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu_0 \ = \ \mbox{die magnetische Feldkonstante oder {\bf Induktionskonstante}}\index{Induktionskonstante} \ $}$](IMG349.GIF) |
|
|
(5.6) |
Sie bilden mit der dualen Geschwindigkeiten 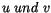 den Elementarwiderstand
des inneren Raums der Impulstheorie:
den Elementarwiderstand
des inneren Raums der Impulstheorie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}v \ \mu_0 \ = \ \displaystyle\frac {...
...}\ = \ \fbox {$\rule[-4mm]{0cm}{1cm}R_M = \mbox{Materiewiderstand \ [Ohm]} \ $}$](IMG352.GIF) |
|
|
(5.7) |
Analog finden wir den Vakuumwiderstand für die Enfernungen 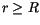 der Dualentheorie:
der Dualentheorie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}c \ \mu_0 \ = \ \displaystyle\frac {...
...$}\ = \ \fbox {$\rule[-4mm]{0cm}{1cm}R_V = \mbox{Vakuumwiderstand \ [Ohm]} \ $}$](IMG354.GIF) |
|
|
(5.8) |
Der Quotient aus elektrostatischen Energie zu kinetischen Energie des Teilchens,
ist gleich dem Quotient des Vakuumwiderstands zum Elementarwiderstand, der mit
Sommerfeldschen Feinstruckturkonstante bezeichnet wird.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {R_V}{R_M} \ = \ ...
...style\frac {1}{c \varepsilon_0}) \ \ (\displaystyle\frac {Z \ e^2}{2 \ h}) \ $}$](IMG355.GIF) |
|
|
(5.9) |
Der experimentell gefundene Wert des Elementarwiderstands durch seinen
Entdecker
K. Von-Klitzing5.2 ist um den Faktor zwei kleiner als die Größe des Elementarwiderstands in der
dualen Physik. Der Faktor zwei ist auf die zweifache Elementarwirkung (4.67)
zurückzuführen.
ist um den Faktor zwei kleiner als die Größe des Elementarwiderstands in der
dualen Physik. Der Faktor zwei ist auf die zweifache Elementarwirkung (4.67)
zurückzuführen.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mbox{Hall-Widerstand} \ = \ (\displaystyle\frac {h}{Z \ e^2}) \ \ \ \ mit \ Z \ = \ 1,2,3,....n \ $}$](IMG358.GIF) |
|
|
(5.10) |
Unterabschnitte





Nächste Seite: Der elektromagnetische Viererimpuls der
Aufwärts: Das positive, negative und
Vorherige Seite: Das positive, negative und
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_j \ = \ ( \ i\phi^- \ , \ \ \displ...
...\displaystyle\frac {As}{m} \ \quad \mbox{\bf Das Viererpotential der IT} \ \ $}$](IMG337.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_j \ = \ ( \ i\phi^- \ , \ \ \displ...
...\displaystyle\frac {As}{m} \ \quad \mbox{\bf Das Viererpotential der IT} \ \ $}$](IMG337.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}a^j \ = \ ( \ \displaystyle\frac {\v...
... \displaystyle\frac {Vs}{m} \ \quad \mbox{\bf Das Viererpotential de ET} \ \ $}$](IMG341.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\widehat{A}_j \ = \ ( \ i\widehat{\p...
...\ \displaystyle\frac {Vs}{m} \ \ \mbox{\bf Das Viererkernpotential der IT} \ $}$](IMG346.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\widehat{a}^j \ = \ ( \ \displaystyl...
...\ \displaystyle\frac {As}{m} \ \ \mbox{\bf Das Viererkernpotential der ET} \ $}$](IMG347.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varepsilon_0 \ = \ \mbox{die elektrische Feldkonstante oder {\bf Influenzkonstante}}\index{Influenzkonstante} \ $}$](IMG348.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu_0 \ = \ \mbox{die magnetische Feldkonstante oder {\bf Induktionskonstante}}\index{Induktionskonstante} \ $}$](IMG349.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}v \ \mu_0 \ = \ \displaystyle\frac {...
...}\ = \ \fbox {$\rule[-4mm]{0cm}{1cm}R_M = \mbox{Materiewiderstand \ [Ohm]} \ $}$](IMG352.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}c \ \mu_0 \ = \ \displaystyle\frac {...
...$}\ = \ \fbox {$\rule[-4mm]{0cm}{1cm}R_V = \mbox{Vakuumwiderstand \ [Ohm]} \ $}$](IMG354.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {R_V}{R_M} \ = \ ...
...style\frac {1}{c \varepsilon_0}) \ \ (\displaystyle\frac {Z \ e^2}{2 \ h}) \ $}$](IMG355.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mbox{Hall-Widerstand} \ = \ (\displaystyle\frac {h}{Z \ e^2}) \ \ \ \ mit \ Z \ = \ 1,2,3,....n \ $}$](IMG358.GIF)