




Nächste Seite: Das elektromagnetische Wirkungsintegral der
Aufwärts: Das duale Viererpotential
Vorherige Seite: Der elektromagnetische Viererimpuls der
Inhalt
Index
Aus der Analogie zur Impulstheorie schreiben wir für den Viererfeldimpuls
der Energietheorie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( \displaystyle\frac {\pa...
... e \ ( \ \displaystyle\frac {\varphi^+}{c}\ \ , \ \ i\vec{a^-} \ ) \ \quad \ $}$](IMG372.GIF) |
|
|
(5.17) |
Analog zu IT schreiben wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \partial^k \ = \ e \ a^j\ \quad : \quad r \leq K^{-1} \quad \ $}$](IMG373.GIF) |
|
|
(5.18) |
Hier haben wir bereits den Faktor (
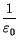 ) in den Vierervektor
integriert.
Für das Viererimplus des Kernbreiches in der ET (
) in den Vierervektor
integriert.
Für das Viererimplus des Kernbreiches in der ET (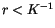 ) finden wir:
) finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( \displaystyle\frac {\pa...
...style\frac {\widehat{\varphi}^+}{c}\ \ , \ \ i\widehat{\vec{a}}^-\ ) \quad \ $}$](IMG376.GIF) |
|
|
(5.19) |
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( \displaystyle\frac {\pa...
... e \ ( \ \displaystyle\frac {\varphi^+}{c}\ \ , \ \ i\vec{a^-} \ ) \ \quad \ $}$](IMG372.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( \displaystyle\frac {\pa...
... e \ ( \ \displaystyle\frac {\varphi^+}{c}\ \ , \ \ i\vec{a^-} \ ) \ \quad \ $}$](IMG372.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \partial^k \ = \ e \ a^j\ \quad : \quad r \leq K^{-1} \quad \ $}$](IMG373.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( \displaystyle\frac {\pa...
...style\frac {\widehat{\varphi}^+}{c}\ \ , \ \ i\widehat{\vec{a}}^-\ ) \quad \ $}$](IMG376.GIF)