Das elekromagnetische Wirkungsintegral

der Impulstheorie

Die Wirkung eines freien Teilchens haben wir schon unter (4.1.2) und (4.1.5) abgehandelt. Der Integrand des Wirkungsintegrals ist ein Skalar, der aus dem skalaren Produkt der elektromagnetischen Viererimpuls und des infinitesimalen Viererortsvektors gewonnen wird. Für die Energietheorie können wir schreiben:

$$\fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \ = \ ( e \ R_V ) \displaystyle\int \ ( \ i\phi^- \ , \ \ \displaystyle\frac {\vec{A}^+}{c}\ ) \ dX_k \quad\ $}$$ (5.20)

Für die Entfernungen 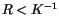$R<K^{-1}$ erhalten wir:

$$\fbox {$\rule[-4mm]{0cm}{1cm}- \hbar_K \ = \ ( e \ \displaystyle\... ...\phi}^-\ , \ \ \displaystyle\frac {\widehat{\vec{A}}^+}{c}\ ) \ dX_k \quad \ $}$$ (5.21)