




Nächste Seite: Der elektromagnetische Viererimpuls der
Aufwärts: Das duale Viererpotential
Vorherige Seite: Das duale Viererpotential
Inhalt
Index
Die Wechselwirkung der Elementarladung mit einer elektromagnetischen
Umgebung wird durch die Komponenten des Viererimpulses, die potentielle
Enegie und der elektromagnetische Impuls beschrieben.
Analog zu dem mechanischen Impuls lautet diese Beziehung:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( i\displaystyle\frac {\p...
...\ = \ ( e \ R_V ) \ ( \ i\phi^- \ , \ \displaystyle\frac {\vec{A}^+}{c}\ ) \ $}$](IMG359.GIF) |
|
|
(5.11) |
Oder in einer anderen Darstellung :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \partial_k \ = \ (e R_V) \ A_j \qquad $}$](IMG360.GIF) |
|
|
(5.12) |
Für die Entfernungen 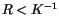 wie bereits im Viererpotential erwähnt,
ist der folgende Hinweis von Nutzen :
wie bereits im Viererpotential erwähnt,
ist der folgende Hinweis von Nutzen :
Die Anzahl der Feldlinien oder der Fluß 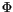 ist ein Maß für die Feldstärke
und so für die Kraft, die ein Teilchen beim Durchflug dieses Feldes erfährt.
Beim eindringen in den Atomkern verstärkt sich dieser Fluß
um den Faktor
ist ein Maß für die Feldstärke
und so für die Kraft, die ein Teilchen beim Durchflug dieses Feldes erfährt.
Beim eindringen in den Atomkern verstärkt sich dieser Fluß
um den Faktor 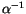 und die entsprechende Kraft um den Faktor
und die entsprechende Kraft um den Faktor 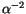 .
.
Mit dieser Klarstellung können wir für den inneren Raum 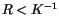 der IT schreiben:
der IT schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( i\displaystyle\frac {\p...
... \ i\widehat{\phi}^-\ , \ \ \displaystyle\frac {\widehat{\vec{A}}^+}{c}\ ) \ $}$](IMG364.GIF) |
|
|
(5.13) |
In (5.13) ist 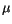 die äquivalente magnetische Ladung der
Impulstheorie :
die äquivalente magnetische Ladung der
Impulstheorie :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu \ = \ ( e \ R_M ) \ = \ [ Vs ] \ \ $}$](IMG366.GIF) |
|
|
(5.14) |
Seine Grenzwerte finden wir aus der Beziehung
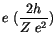 :
:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu \ = \ \left\{ \begin{array}{r@{\...
...2 h}{e^2}) & Z = 1 \vspace{0.3em}\\ 0 \ & Z = \infty \end{array} \right.\ \ $}$](IMG368.GIF) |
|
|
(5.15) |
Mit wachsender Kernladungszahl 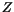 verkleinert sich die magnetische
Ladung um den Faktor
verkleinert sich die magnetische
Ladung um den Faktor 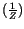 . Aus der
Kernphysik wissen wir, daß mit steigender Kernladungszahl die Kernkraft
abnimmt. Die schweren Kerne in der Natur kommen deshalb nicht vor und zerfallen
in die leichteren Töchterkerne.
Eine andere Darstellung dieser Beziehung lautet:
. Aus der
Kernphysik wissen wir, daß mit steigender Kernladungszahl die Kernkraft
abnimmt. Die schweren Kerne in der Natur kommen deshalb nicht vor und zerfallen
in die leichteren Töchterkerne.
Eine andere Darstellung dieser Beziehung lautet:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \partial^k \ = \ \mu \ \widehat{A}_j \quad : \quad R < K^{-1} \quad $}$](IMG371.GIF) |
|
|
(5.16) |





Nächste Seite: Der elektromagnetische Viererimpuls der
Aufwärts: Das duale Viererpotential
Vorherige Seite: Das duale Viererpotential
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( i\displaystyle\frac {\p...
...\ = \ ( e \ R_V ) \ ( \ i\phi^- \ , \ \displaystyle\frac {\vec{A}^+}{c}\ ) \ $}$](IMG359.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( i\displaystyle\frac {\p...
...\ = \ ( e \ R_V ) \ ( \ i\phi^- \ , \ \displaystyle\frac {\vec{A}^+}{c}\ ) \ $}$](IMG359.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \partial_k \ = \ (e R_V) \ A_j \qquad $}$](IMG360.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \Big( i\displaystyle\frac {\p...
... \ i\widehat{\phi}^-\ , \ \ \displaystyle\frac {\widehat{\vec{A}}^+}{c}\ ) \ $}$](IMG364.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu \ = \ ( e \ R_M ) \ = \ [ Vs ] \ \ $}$](IMG366.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu \ = \ \left\{ \begin{array}{r@{\...
...2 h}{e^2}) & Z = 1 \vspace{0.3em}\\ 0 \ & Z = \infty \end{array} \right.\ \ $}$](IMG368.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar \partial^k \ = \ \mu \ \widehat{A}_j \quad : \quad R < K^{-1} \quad $}$](IMG371.GIF)