




Nächste Seite: Das Variationsprinzip der Impulstheorie
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Der Viererimpuls der Impulstheorie
Inhalt
Index
Das Drehimpulsintegral wird häufig als das Wirkungsintegral bezeichnet.
Obwohl diese Bezeichnung nicht zutreffend ist, werden wir sie doch beibehalten.
Die Wirkung
ist eine invariante bezüglich des dualen4.3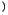 Bezugssytems. Die
physikalische Schlußfolgerung aus dieser außerordentlich wichtigen Erkenntnis
ist unter anderem, die Bezugssystemunabhängigkeit der Konstante
Bezugssytems. Die
physikalische Schlußfolgerung aus dieser außerordentlich wichtigen Erkenntnis
ist unter anderem, die Bezugssystemunabhängigkeit der Konstante 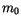 ,
die
als Teilchen-Ruhemasse seine mechanischen Eigenschaften darstellt. Es gilt daher
die Beziehung :
,
die
als Teilchen-Ruhemasse seine mechanischen Eigenschaften darstellt. Es gilt daher
die Beziehung :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_j^k = (m_0 c) \ \delta_j^k \ \ \ \ \ $}$](IMG213.GIF) |
|
|
(4.9) |
Die Komponente des Viererwirkungsintegrals der Impulstheorie lautet :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}S_k^1 = P_1^k \ \displaystyle\int \l...
...\quad = \quad
P_1^k \ \displaystyle\int \limits_{X_i} dX_{1k} \ . \ U_{kj} \ $}$](IMG214.GIF) |
|
|
(4.10) |
oder auch in der einfacheren Form
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}- S = m_0 c \ \displaystyle\int \limits^{L_2}_{L_1} dR \ \sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}\ $}$](IMG215.GIF) |
|
|
(4.11) |
Um die Größenordnung der Wirkungsinvariante 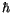 abzuschätzen, errechnen
wir zuerst den Integrand in (4.10) aus. Für das Viererintegral erhalten wir :
abzuschätzen, errechnen
wir zuerst den Integrand in (4.10) aus. Für das Viererintegral erhalten wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-S = -\displaystyle\int \limits_{c {...
...\ \ m = \displaystyle\frac {m_0}{\sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}}$](IMG216.GIF) |
|
|
(4.12) |
Seiner Zeit haben wir die duale Einheit 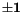 durch das Produkt
durch das Produkt
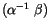 festgelegt. Für die zeitabhängigen Therme
führen wir
festgelegt. Für die zeitabhängigen Therme
führen wir
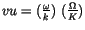 ein
4.4
ein
4.4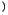 . Die differentielle
Form dieser Beziehung lautet :
. Die differentielle
Form dieser Beziehung lautet :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dR}{cdT} \ \disp...
...ac {dr}{cdt} = \displaystyle\frac {dR}{cdt} \ \displaystyle\frac {dr}{cdT} \ $}$](IMG223.GIF) |
|
|
(4.13) |
Folglich erhalten wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dR}{cdt} \ = \ \...
...\quad \displaystyle\frac {dR}{cdt} \ = \ \displaystyle\frac {dr}{cdT} = -1 \ $}$](IMG224.GIF) |
|
|
(4.14) |
Mit der linken Seite von (4.14) können wir für die Lichtgeschwindigkeit schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dR}{dt} = c = \d...
...ac {\omega}{K} \ \ \ \ mit \ \ \ \ K = \displaystyle\frac {2 \pi}{\Lambda} \ $}$](IMG225.GIF) |
|
|
(4.15) |
und mit der rechten Seite von (4.14) finden wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dr}{dT} = c = \d...
...ac {\Omega}{k} \ \ \ \ mit \ \ \ \ k = \displaystyle\frac {2 \pi}{\lambda} \ $}$](IMG226.GIF) |
|
|
(4.16) |
Mit Hilfe von (4.16) und 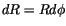 schreiben wir die beiden Terme um und
erhalten schließlich unter der Berücksichtigung, daß die
Wirkung im Koordinatenursprung und im Unendlichen verschwindet:
schreiben wir die beiden Terme um und
erhalten schließlich unter der Berücksichtigung, daß die
Wirkung im Koordinatenursprung und im Unendlichen verschwindet:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-S = - \displaystyle\frac {1}{2\pi}\...
...yle\int \limits_{\phi_1=0}^{\phi_2=2\pi} \{ m c \ Rd\phi \} \ \right) \qquad $}$](IMG228.GIF) |
|
|
(4.17) |
Aus der Invarianz des dualen Abstands schließen wir auf die Invarianz
der dualen Wirkungsintegrale. Folglich erhalten wir :
Die gesuchte Invaiante wie letztlich vereinbart wurde (s. (1.1.1)), hat die Dimension
![$[VAs^2]$](IMG230.GIF) und kann nur der Quant
und kann nur der Quant 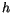 sein, der nach seinem Entdecker Max Planck
das Planksche Wirkungsquantum
genannt wird.
Unter der Berücksichtigung, daß die Wirkung eine endliche Größe ist,
erhalten wir nach der Integration der Gleichung (4.17) schließlich :
sein, der nach seinem Entdecker Max Planck
das Planksche Wirkungsquantum
genannt wird.
Unter der Berücksichtigung, daß die Wirkung eine endliche Größe ist,
erhalten wir nach der Integration der Gleichung (4.17) schließlich :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}S \ = \ \Big( \ \displaystyle\frac {...
... \, m c \ R \, \} \ \ \ mit \ \ \ \lambda \equiv 2 \pi l \ \ \ oder \ \ ...\ $}$](IMG232.GIF) |
|
|
(4.18) |
Erwartungsgemäß liefert das zeitabhängige Glied mit 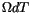 den
Term mit der Welleneigenschaft. Er ist unabhängig von der Ausdehnug der
jeweiligen Welle. Der zweite Term ist ortsabhängig und gibt den
Drehimpulscharakter wieder. Er ist unanhängig von den Änderungen des Ortsvektors.
Die Anpassung an die linke Seite dieser Gleichung können wir aus den Beziehungen
den
Term mit der Welleneigenschaft. Er ist unabhängig von der Ausdehnug der
jeweiligen Welle. Der zweite Term ist ortsabhängig und gibt den
Drehimpulscharakter wieder. Er ist unanhängig von den Änderungen des Ortsvektors.
Die Anpassung an die linke Seite dieser Gleichung können wir aus den Beziehungen
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}S \ \geq \ \left( \ \displaystyle\fr...
...ule[-4mm]{0cm}{1cm}S \, \geq \ \left(\, \hbar \, - \, s\hbar\, \right) \quad $}$](IMG234.GIF) |
|
|
(4.19) |
entnehmen.
Der Faktor 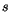 ist die sogenannte Spin-Quantenzahl. Für die ganzzahligen
ist die sogenannte Spin-Quantenzahl. Für die ganzzahligen
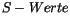 erwartet man aus der ersten Beziehung mit
Heisenbergscher Unbestimmtheitsrelation (UBR)
erwartet man aus der ersten Beziehung mit
Heisenbergscher Unbestimmtheitsrelation (UBR)
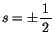 und aus der
zweiten Beziehung mit der De Broglie Welle
und aus der
zweiten Beziehung mit der De Broglie Welle 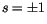 .
.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar \ \leq \ \left( \displaystyle\...
... { m v \ \lambda }{2\pi} \right) \ \quad \mbox{{\bf De Broglie Welle}} \quad $}$](IMG239.GIF) |
|
|
(4.20) |
und für den zweiten Summand des Spinquants
erhalten wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( s\, \hbar \right) \ \leq \ \{ \ m c \ R \ \} \quad \ \mbox{\bf der \ Spin-Quant} \quad $}$](IMG240.GIF) |
|
|
(4.21) |





Nächste Seite: Das Variationsprinzip der Impulstheorie
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Der Viererimpuls der Impulstheorie
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_j^k = (m_0 c) \ \delta_j^k \ \ \ \ \ $}$](IMG213.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_j^k = (m_0 c) \ \delta_j^k \ \ \ \ \ $}$](IMG213.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}S_k^1 = P_1^k \ \displaystyle\int \l...
...\quad = \quad
P_1^k \ \displaystyle\int \limits_{X_i} dX_{1k} \ . \ U_{kj} \ $}$](IMG214.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}- S = m_0 c \ \displaystyle\int \limits^{L_2}_{L_1} dR \ \sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}\ $}$](IMG215.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-S = -\displaystyle\int \limits_{c {...
...\ \ m = \displaystyle\frac {m_0}{\sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}}$](IMG216.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dR}{cdT} \ \disp...
...ac {dr}{cdt} = \displaystyle\frac {dR}{cdt} \ \displaystyle\frac {dr}{cdT} \ $}$](IMG223.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dR}{cdt} \ = \ \...
...\quad \displaystyle\frac {dR}{cdt} \ = \ \displaystyle\frac {dr}{cdT} = -1 \ $}$](IMG224.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dR}{dt} = c = \d...
...ac {\omega}{K} \ \ \ \ mit \ \ \ \ K = \displaystyle\frac {2 \pi}{\Lambda} \ $}$](IMG225.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {dr}{dT} = c = \d...
...ac {\Omega}{k} \ \ \ \ mit \ \ \ \ k = \displaystyle\frac {2 \pi}{\lambda} \ $}$](IMG226.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-S = - \displaystyle\frac {1}{2\pi}\...
...yle\int \limits_{\phi_1=0}^{\phi_2=2\pi} \{ m c \ Rd\phi \} \ \right) \qquad $}$](IMG228.GIF)
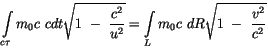
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}S \ = \ \Big( \ \displaystyle\frac {...
... \, m c \ R \, \} \ \ \ mit \ \ \ \lambda \equiv 2 \pi l \ \ \ oder \ \ ...\ $}$](IMG232.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}S \ \geq \ \left( \ \displaystyle\fr...
...ule[-4mm]{0cm}{1cm}S \, \geq \ \left(\, \hbar \, - \, s\hbar\, \right) \quad $}$](IMG234.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar \ \leq \ \left( \displaystyle\...
... { m v \ \lambda }{2\pi} \right) \ \quad \mbox{{\bf De Broglie Welle}} \quad $}$](IMG239.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( s\, \hbar \right) \ \leq \ \{ \ m c \ R \ \} \quad \ \mbox{\bf der \ Spin-Quant} \quad $}$](IMG240.GIF)