




Nächste Seite: Die Wirkung in der
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Das Prinzip der kleinsten
Inhalt
Index
Zwischen zwei Punkten 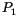 und
und 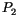 liegende Verbindungskurven bestimmen wir
derart, daß ihre Länge
liegende Verbindungskurven bestimmen wir
derart, daß ihre Länge  minimal wird. Die Länge dieser Kurve
(infinitesimale Länge)
ist offenbar ein Viererskalar und daher ist sie invariant gegenüber Drehungen
des Vierdimensionalen Koordinatensystems. Für das Quadrat des Viererabstandstensors
in der Impulstheorie finden wir :
minimal wird. Die Länge dieser Kurve
(infinitesimale Länge)
ist offenbar ein Viererskalar und daher ist sie invariant gegenüber Drehungen
des Vierdimensionalen Koordinatensystems. Für das Quadrat des Viererabstandstensors
in der Impulstheorie finden wir :
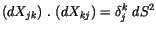 |
|
|
(4.1) |
Dividieren wir die Komponente dieser Gleichung durch den Skalar 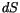 , so erhalten
wir bis auf eine konstante Größe den Integrand des Viererdrehimpulses :
, so erhalten
wir bis auf eine konstante Größe den Integrand des Viererdrehimpulses :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(U_{jk}) \ . \ (dX_{kj}) = \delta_j^k \ dS \ \ \ \ \ mit \ \ \ U_{1k} = \displaystyle\frac {dX_{1k}}{dS} \ \ $}$](IMG196.GIF) |
|
|
(4.2) |
Die Komponenten dieses Tensors (der Viererdrehimpusintegrand) bilden wir
aus den Skalaren
(4.2) und dem Teilchen speziffischen Vierertensor 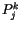 derart, daß dieses
Produkt die
Dimension
derart, daß dieses
Produkt die
Dimension
![$\bf [joule \ sec]$](IMG198.GIF) hat. Bezeichnen wir die Komponente des
Viererdrehimpulstensors mit
hat. Bezeichnen wir die Komponente des
Viererdrehimpulstensors mit 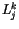 so können
wir für seine Differentiale schreiben:
so können
wir für seine Differentiale schreiben:
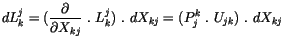 |
|
|
(4.3) |
Aus dem Vergleich der beiden Seiten finden wir :
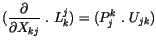 |
|
|
(4.4) |
Für seine Komponenten erhalten wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{\partial X_{k1}}\ L_k^1 = ( i p \ \ , \ \ \vec{P} ) \ \ $}$](IMG202.GIF) |
|
|
(4.5) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}mit \ \ \ p = \displaystyle\frac {m_...
...e\frac {( m_0c ) \vec{t}}{\sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}} \ \ $}$](IMG203.GIF) |
|
|
(4.6) |
Aus der Gleichung (4.5) erkennt man, daß 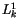 ein Skalar ist, sonst
würde auf der rechten Seite für das Produkt zweier Vierervektoren ein Viererskalar
stehen, was ein Widerspruch zu der linken Seite wäre. Daraus folgt wie schon
oben erwähnt: Die Wirkung ist eine skalare Größe, die im Bezug des dualen
Bezugssystems eine Invariante darstellt. Weiterhin schließen wir, daß die
partiellen Ableitungen der Wirkung nach der Viererkoordinaten in (4.5) verschwinden,
was ebenfalls ein Widerspruch zu der rechten Seite ist. Das Dilemma lässt
sich beheben, falls man die linke Seite dieser Gleichung als Impulsoperator
oder das Produkt der Drehimpulsinvariante4.2
ein Skalar ist, sonst
würde auf der rechten Seite für das Produkt zweier Vierervektoren ein Viererskalar
stehen, was ein Widerspruch zu der linken Seite wäre. Daraus folgt wie schon
oben erwähnt: Die Wirkung ist eine skalare Größe, die im Bezug des dualen
Bezugssystems eine Invariante darstellt. Weiterhin schließen wir, daß die
partiellen Ableitungen der Wirkung nach der Viererkoordinaten in (4.5) verschwinden,
was ebenfalls ein Widerspruch zu der rechten Seite ist. Das Dilemma lässt
sich beheben, falls man die linke Seite dieser Gleichung als Impulsoperator
oder das Produkt der Drehimpulsinvariante4.2
 mit dem Vierergradient, der als Viererimpuls bezeichnet wird, auffasst.
mit dem Vierergradient, der als Viererimpuls bezeichnet wird, auffasst.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar_k^1 \displaystyle\frac {\parti...
...\partial X_{k1}}= P_j \ \ \ mit \ \ \ \hbar_k^1 = \delta_k^1 \ \hbar \quad \ $}$](IMG207.GIF) |
|
|
(4.7) |
Der Vergleich der beiden Seiten von (4.5) mit
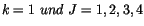 liefert :
liefert :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i\hbar\displaystyle\frac {\partial}...
...rtial}{\partial Y}, \ \displaystyle\frac {\partial}{\partial Z}) = \vec{P} \ $}$](IMG209.GIF) |
|
|
(4.8) |
Das Quadrat des Viererimpulses ist eine Invariante. Als Beweis quadrieren wir
die Gleichung (4.7) und erhalten:
Für die rechte Seite gilt die Beziehung :





Nächste Seite: Die Wirkung in der
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Das Prinzip der kleinsten
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(U_{jk}) \ . \ (dX_{kj}) = \delta_j^k \ dS \ \ \ \ \ mit \ \ \ U_{1k} = \displaystyle\frac {dX_{1k}}{dS} \ \ $}$](IMG196.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{\partial X_{k1}}\ L_k^1 = ( i p \ \ , \ \ \vec{P} ) \ \ $}$](IMG202.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}mit \ \ \ p = \displaystyle\frac {m_...
...e\frac {( m_0c ) \vec{t}}{\sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}} \ \ $}$](IMG203.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar_k^1 \displaystyle\frac {\parti...
...\partial X_{k1}}= P_j \ \ \ mit \ \ \ \hbar_k^1 = \delta_k^1 \ \hbar \quad \ $}$](IMG207.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i\hbar\displaystyle\frac {\partial}...
...rtial}{\partial Y}, \ \displaystyle\frac {\partial}{\partial Z}) = \vec{P} \ $}$](IMG209.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P^2 \ - \ p^2 \ = \ m_0^2 c^2 \ \ $}$](IMG211.GIF)