Die Eigenwerte der Energietheorie

In diesem Kapitel behandeln wir analog zu IT das kräftefreie Teilchen und benutzen die Gleichungen:

$$\fbox {$\rule[-4mm]{0cm}{1cm}\hbar^2\, (\, \partial^{1k}\, . \, \partial^{jk}\, ) \ = \ (\, p^{k1} \ . \ p^{kj}\, ) \quad $}$$ (10.1)

Errechnen wir die Klammer auf beiden Seiten aus, so finden wir mit 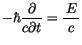$-\hbar\displaystyle\frac {\partial}{c \partial t}= \displaystyle\frac {\, E\, }{c}$ und $P^2 \, - \, P_0^2 \ = \ p^2$:

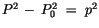$$\fbox {$\rule[-4mm]{0cm}{1cm}\hbar^2 \, {\sf grad}^2 \, + \, (\, (\displaystyle\frac {\, E\, }{c})^2 \ - \ P_0^2\, ) \ = \ 2 p^2 \quad $}$$ (10.2)

Die Gleichung (10.2) ist die Differentialgleichung des kräftefreien Teilchens der ET. Multiplizieren wir diese Gleichung mit der Wellenfunktion 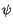$\psi$, so erhalten wir analog zu der IT die Wellengleichung des Rotators.

$$\fbox {$\rule[-4mm]{0cm}{1cm}(\, \hbar^2 \, {\sf grad}^2 \, + \, ... ...le\frac {\, E\, }{c})^2 \ - \ P_0^2\, )\, )\, \psi \ = \ 2 p^2 \, \Psi \quad $}$$ (10.3)

Um sie zu lösen, werden wir zuerst die kartesische Koordinaten in Kugelkoordinaten überführen, welches unser Ziel im nächsten Abschnitt ist.