



Nächste Seite: Die Eigenwerte der Kugelfunktionen
Aufwärts: Die Eigenwerte der Energietheorie
Vorherige Seite: Die Eigenwerte der Energietheorie
Inhalt
Index
Die Kugelfunktionen in der ET
Die kartesischen Koordinaten lassen sich durch Transformationen in
Polarkoordinaten umwandeln. Die Darstellung eines Punktes bezüglich der
zwei Systeme sind dann durch die folgenden Beziehungen miteinander verknüpft:
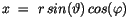 |
|
|
(10.4) |
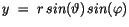 |
|
|
(10.5) |
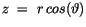 |
|
|
(10.6) |
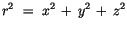 |
|
|
(10.7) |
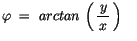 |
|
|
(10.8) |
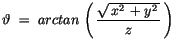 |
|
|
(10.9) |
Jede infinitesimale Änderungen der Variabeln
 der
kartesischen Koordinaten führt zu einer
afinen Transfomation der Polarkoordinaten und damit zur Änderungen der
Variabeln
der
kartesischen Koordinaten führt zu einer
afinen Transfomation der Polarkoordinaten und damit zur Änderungen der
Variabeln
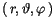 . Nun werden wir die Matrix dieser
Transformationen an Hand der Gleichungen (10.4), (10.5), und (10.6) ableiten. Differenzieren
wir diese Gleichungen, so stellen wir fest, daß folgende Differentialquotienten
bei der Ableitungen der kartesischen Variabeln die Komponenten der
gesuchte Transformationmatrix ergeben:
. Nun werden wir die Matrix dieser
Transformationen an Hand der Gleichungen (10.4), (10.5), und (10.6) ableiten. Differenzieren
wir diese Gleichungen, so stellen wir fest, daß folgende Differentialquotienten
bei der Ableitungen der kartesischen Variabeln die Komponenten der
gesuchte Transformationmatrix ergeben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{1k} \ = \ \left( \ 0 \ , \ \ (\di...
...artial r}y)\ , \ (\displaystyle\frac {\partial}{\partial r}z)\, \right)\quad $}$](IMG701.GIF) |
|
|
(10.10) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{1k} \ = \ \left( \ 0 \ , ...
...rac {1}{r}\displaystyle\frac {\partial}{\partial \vartheta}z)\, \right)\quad $}$](IMG702.GIF) |
|
|
(10.11) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{1k} \ = \ \left( \ 0 \ , \ ...
...(\vartheta)}\displaystyle\frac {\partial}{\partial \varphi}z)\, \right)\quad $}$](IMG703.GIF) |
|
|
(10.12) |
Nach Ausführung der Differentiation erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{1k} \ = \ \left( \ 0 \ , \ \ (sin...
...))\ , \ (sin(\vartheta)\, sin(\varphi))\ , \ (cos(\vartheta))\, \right)\quad $}$](IMG704.GIF) |
|
|
(10.13) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{1k} \ = \ \left( \ 0 \ , ...
...)\ , \ (cos(\vartheta)\, sin(\varphi))\ , \ -(sin(\vartheta))\, \right)\quad $}$](IMG705.GIF) |
|
|
(10.14) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{1k} \ = \ \left( \ 0 \ , \ \ -(sin(\varphi))\ , \ (cos(\varphi))\ , \ (\, 0 \, ))\, \right)\quad $}$](IMG706.GIF) |
|
|
(10.15) |
Die drei Transformationmatrix sind unter sich wie folgt verknüpft:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{jk} \ . \ r^{kj} \ = \ \delta_j^k \quad $}$](IMG707.GIF) |
|
|
(10.16) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{jk} \ . \ \vartheta^{kj} \ = \ \delta_j^k \quad $}$](IMG708.GIF) |
|
|
(10.17) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{jk} \ . \ \varphi^{kj} \ = \ \delta_j^k \quad $}$](IMG709.GIF) |
|
|
(10.18) |
Untereinander weisen sie folgende Eigenschaften auf:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{jk} \ . \ \vartheta^{jk} \ = \ \v...
...box {$\rule[-4mm]{0cm}{1cm}\vartheta^{jk} \ . \ r^{jk} \ = \ \phi^{kj} \quad $}$](IMG710.GIF) |
|
|
(10.19) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{jk} \ . \ \varphi^{jk} \ ...
... {$\rule[-4mm]{0cm}{1cm}\varphi^{jk} \ . \ \vartheta^{jk} \ = \ r^{kj} \quad $}$](IMG711.GIF) |
|
|
(10.20) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{jk} \ . \ r^{jk} \ = \ \var...
... {$\rule[-4mm]{0cm}{1cm}r^{jk} \ . \ \varphi^{jk} \ = \ \vartheta^{kj} \quad $}$](IMG712.GIF) |
|
|
(10.21) |
Bezeichen wir den infinitesimalen polaren Viererortstensor mit 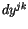 , so
können wir für seine Komponente schreiben:
, so
können wir für seine Komponente schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dy^{1k} \ = \ \left( \, c\, dt \ , \...
...theta\, \ , \ \varphi^{1k}\, r\, sin(\vartheta)\ d\varphi\, )\, \right)\quad $}$](IMG714.GIF) |
|
|
(10.22) |
Die Überführung der kartesischen in Polarkoordinaten wurde realisiert,
in dem wir jeden Komponenten des Linienelements
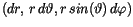 eine explizite orthogonale
Transformationen zugeordnet haben. Die so entstandene Raumelemente sind Komponenten
der polaren Vierertensoren mit den Einheitsvektoren der kartesischen
Koordinaten.
Wir weisen an dieser Stelle besonders darauf hin, daß
im Gegensatz zur kartesischen Koordinaten
eine explizite orthogonale
Transformationen zugeordnet haben. Die so entstandene Raumelemente sind Komponenten
der polaren Vierertensoren mit den Einheitsvektoren der kartesischen
Koordinaten.
Wir weisen an dieser Stelle besonders darauf hin, daß
im Gegensatz zur kartesischen Koordinaten
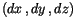 wir mit fünf Variabln
wir mit fünf Variabln
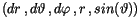 der Polarkoordinaten zu tun haben.
Für das Abstandquadrat erhalten wir unter Berücksichigung von (10.16), (10.17)
und (10.18):
der Polarkoordinaten zu tun haben.
Für das Abstandquadrat erhalten wir unter Berücksichigung von (10.16), (10.17)
und (10.18):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}ds^2 \ = \ (\, c^2\, dt^2\, - \, (\,...
..., r^2\, d\vartheta^2\, + \, r^2\, sin(\vartheta)^2\, d\varphi^2\, )\, )\quad $}$](IMG718.GIF) |
|
|
(10.23) |
Analog zu (10.22) kann man die Vierergradienten der Polarkoordinaten ermitteln.
man findet sie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial^{1k}\ = \ \left(\, \display...
...vartheta)}\displaystyle\frac {\partial}{\partial \varphi}\, )\, \right)\quad $}$](IMG719.GIF) |
|
|
(10.24) |
Dieses Ergebnis in (10.23) kommt der Vorstellung eines orthogonalen polaren
Ortsvektors mit
Einheitsvektoren
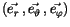 nahe.
Diese Äquivalenz zu den kartesischen Koordinaten bleibt aufrechtenthalten,
solange die Berechnungen (die Tensorprodukte) keine Vierergradienten enthalten.
Hierzu betrachten wir die vereinfachte Gleichung (7.18):
nahe.
Diese Äquivalenz zu den kartesischen Koordinaten bleibt aufrechtenthalten,
solange die Berechnungen (die Tensorprodukte) keine Vierergradienten enthalten.
Hierzu betrachten wir die vereinfachte Gleichung (7.18):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, {\sf div} \displaystyle\frac {\vec{e^+}_{(\vec{r})}}{c}\, \ , \ \ -{\sf rot} \vec{b^-}\, ) \quad $}$](IMG721.GIF) |
|
|
(10.25) |
Man findet oft in der Literatur Integralgleichungen, die zur
Definition10.1 (10.25) der div und rot der Vektoren beitragen:
Nach Gauß - Ostrogradskischen Formel ist das Volumenintegral der div
gleich dem Vektorfluß der Oberfläche des Bereiches:
(10.25) der div und rot der Vektoren beitragen:
Nach Gauß - Ostrogradskischen Formel ist das Volumenintegral der div
gleich dem Vektorfluß der Oberfläche des Bereiches:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf div} \vec{e^+}_{(r,\vartheta,\v...
...yle\oint \vec{e^+}_{(r,\vartheta,\varphi)} . d\vec{f}\, }{\triangle v} \quad $}$](IMG722.GIF) |
|
|
(10.26) |
und nach Stockesschen Formel ist die Zirkulation des Vektorfeldes 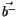 längs der Kontur
längs der Kontur 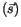 einer Fläche
einer Fläche 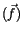 gleich dem Integral der Normalkomponente
der rot über die Fläche selbst, d.h. gleich dem Wirbelfluß durch die
Fläche:
gleich dem Integral der Normalkomponente
der rot über die Fläche selbst, d.h. gleich dem Wirbelfluß durch die
Fläche:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf rot} \vec{b^-}_{(r,\vartheta,\v...
...yle\oint \vec{b^-}_{(r,\vartheta,\varphi)} . d\vec{s}\, }{\triangle f} \quad $}$](IMG726.GIF) |
|
|
(10.27) |
Unsere Beweislage wird sich aber nicht auf diese Gleichungen stützen. Lediglich
werden wir sie zum Vergleich heranziehen.
Wir errechnen zuerst das Volumen und das Flächenelement aus den Komponenten
in (10.22). Man erhält:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dv_1^k \ = \ i dr\, r\, d\vartheta\,...
...) \ = \ i\ r^2\, dr\, d\vartheta\, sin(\vartheta)\, d\varphi \delta_1^k\quad $}$](IMG727.GIF) |
|
|
(10.28) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}d\vec{f} \ = \ -(\, (\, r^2\, sin(\v...
..., )\, \vartheta^{1k}\, \ , (\, r\, dr\, d\vartheta\, )\, \phi^{1k}\, ) \quad $}$](IMG728.GIF) |
|
|
(10.29) |
Nun errechnen wir das Tensorprodukt
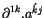 aus:
In
aus:
In
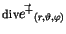 können außer
können außer
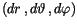 noch
noch 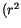 und
und
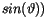 und in
und in
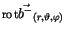 die Größen
die Größen 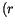 und
und
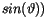 in die Berechnungen eingehen.
Bei der Ableitungen wird die Transformationenmatrix konstant gehalten und nur
ihre Faktoren, des Flächen
in die Berechnungen eingehen.
Bei der Ableitungen wird die Transformationenmatrix konstant gehalten und nur
ihre Faktoren, des Flächen
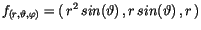 |
|
|
(10.30) |
bzw. des Linienelements
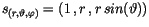 |
|
|
(10.31) |
differenziert. Führen wir die Differenzation durch, so finden wir für den polare
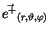 und axialen Vektor
und axialen Vektor
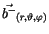
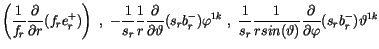 |
|
|
(10.32) |
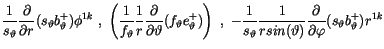 |
|
|
(10.33) |
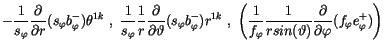 |
|
|
(10.34) |
Berücksichtigen wir diesen Umstand bei der Ableitungen nach
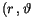 und
und 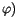 , so finden wir für div eines polaren Vektors
, so finden wir für div eines polaren Vektors
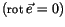 im Fall
der Oberflächenabhängigkeit der Matrix
im Fall
der Oberflächenabhängigkeit der Matrix
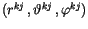 übereinstimmend mit
den Termen in den runden Klammern von (10.32), (10.33) und (10.34):
übereinstimmend mit
den Termen in den runden Klammern von (10.32), (10.33) und (10.34):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf div}\vec{e^+}_{(r,\vartheta,\va...
... sin(\vartheta)}\displaystyle\frac {\partial}{\partial \varphi}e^+_{\varphi} $}$](IMG747.GIF) |
|
|
(10.35) |
Entsprechende Formel erhalten wir für die rot eines axialen Vektors
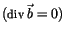 , falls wir die genannten
Matrixen als linear (10.32), (10.33), (10.34) betrachten:
, falls wir die genannten
Matrixen als linear (10.32), (10.33), (10.34) betrachten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf rot} (\vec{b^-}_{(r,\vartheta,\...
...le\frac {\partial}{\partial \vartheta}b^-_r\, ) \phi^{1k} \end{array}\right) $}$](IMG749.GIF) |
|
|
(10.36) |
Äquivalent zu div kann man den Laplace Operator ableiten. Analog zu
(10.33) erhalten wir für das Drehimpulsquadrat:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\hbar {\sf grad})^2 = -\hbar^2 \lef...
...{r sin(\vartheta)}\displaystyle\frac {\partial}{\partial \varphi})^2 \right) $}$](IMG750.GIF) |
|
|
(10.37) |
Diese, sind die Differentialgleichungen der Kugelfuntionen.
Sie werden in radialen und winkelabhängigen Kugelfunktionen unterteilt.




Nächste Seite: Die Eigenwerte der Kugelfunktionen
Aufwärts: Die Eigenwerte der Energietheorie
Vorherige Seite: Die Eigenwerte der Energietheorie
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{1k} \ = \ \left( \ 0 \ , \ \ (\di...
...artial r}y)\ , \ (\displaystyle\frac {\partial}{\partial r}z)\, \right)\quad $}$](IMG701.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{1k} \ = \ \left( \ 0 \ , ...
...rac {1}{r}\displaystyle\frac {\partial}{\partial \vartheta}z)\, \right)\quad $}$](IMG702.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{1k} \ = \ \left( \ 0 \ , \ ...
...(\vartheta)}\displaystyle\frac {\partial}{\partial \varphi}z)\, \right)\quad $}$](IMG703.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{1k} \ = \ \left( \ 0 \ , \ \ (sin...
...))\ , \ (sin(\vartheta)\, sin(\varphi))\ , \ (cos(\vartheta))\, \right)\quad $}$](IMG704.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{1k} \ = \ \left( \ 0 \ , ...
...)\ , \ (cos(\vartheta)\, sin(\varphi))\ , \ -(sin(\vartheta))\, \right)\quad $}$](IMG705.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{1k} \ = \ \left( \ 0 \ , \ \ -(sin(\varphi))\ , \ (cos(\varphi))\ , \ (\, 0 \, ))\, \right)\quad $}$](IMG706.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{jk} \ . \ r^{kj} \ = \ \delta_j^k \quad $}$](IMG707.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{jk} \ . \ \vartheta^{kj} \ = \ \delta_j^k \quad $}$](IMG708.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{jk} \ . \ \varphi^{kj} \ = \ \delta_j^k \quad $}$](IMG709.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r^{jk} \ . \ \vartheta^{jk} \ = \ \v...
...box {$\rule[-4mm]{0cm}{1cm}\vartheta^{jk} \ . \ r^{jk} \ = \ \phi^{kj} \quad $}$](IMG710.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\vartheta^{jk} \ . \ \varphi^{jk} \ ...
... {$\rule[-4mm]{0cm}{1cm}\varphi^{jk} \ . \ \vartheta^{jk} \ = \ r^{kj} \quad $}$](IMG711.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varphi^{jk} \ . \ r^{jk} \ = \ \var...
... {$\rule[-4mm]{0cm}{1cm}r^{jk} \ . \ \varphi^{jk} \ = \ \vartheta^{kj} \quad $}$](IMG712.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dy^{1k} \ = \ \left( \, c\, dt \ , \...
...theta\, \ , \ \varphi^{1k}\, r\, sin(\vartheta)\ d\varphi\, )\, \right)\quad $}$](IMG714.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}ds^2 \ = \ (\, c^2\, dt^2\, - \, (\,...
..., r^2\, d\vartheta^2\, + \, r^2\, sin(\vartheta)^2\, d\varphi^2\, )\, )\quad $}$](IMG718.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial^{1k}\ = \ \left(\, \display...
...vartheta)}\displaystyle\frac {\partial}{\partial \varphi}\, )\, \right)\quad $}$](IMG719.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, {\sf div} \displaystyle\frac {\vec{e^+}_{(\vec{r})}}{c}\, \ , \ \ -{\sf rot} \vec{b^-}\, ) \quad $}$](IMG721.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf div} \vec{e^+}_{(r,\vartheta,\v...
...yle\oint \vec{e^+}_{(r,\vartheta,\varphi)} . d\vec{f}\, }{\triangle v} \quad $}$](IMG722.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf rot} \vec{b^-}_{(r,\vartheta,\v...
...yle\oint \vec{b^-}_{(r,\vartheta,\varphi)} . d\vec{s}\, }{\triangle f} \quad $}$](IMG726.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dv_1^k \ = \ i dr\, r\, d\vartheta\,...
...) \ = \ i\ r^2\, dr\, d\vartheta\, sin(\vartheta)\, d\varphi \delta_1^k\quad $}$](IMG727.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}d\vec{f} \ = \ -(\, (\, r^2\, sin(\v...
..., )\, \vartheta^{1k}\, \ , (\, r\, dr\, d\vartheta\, )\, \phi^{1k}\, ) \quad $}$](IMG728.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf div}\vec{e^+}_{(r,\vartheta,\va...
... sin(\vartheta)}\displaystyle\frac {\partial}{\partial \varphi}e^+_{\varphi} $}$](IMG747.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\sf rot} (\vec{b^-}_{(r,\vartheta,\...
...le\frac {\partial}{\partial \vartheta}b^-_r\, ) \phi^{1k} \end{array}\right) $}$](IMG749.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\hbar {\sf grad})^2 = -\hbar^2 \lef...
...{r sin(\vartheta)}\displaystyle\frac {\partial}{\partial \varphi})^2 \right) $}$](IMG750.GIF)