




Nächste Seite: Das Variationsprinzip der Energietheorie
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Der Viererimpuls der Energietheorie
Inhalt
Index
Analog zu der Impulstheorie ist die Konstante 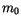 eine Invariante, die
mechanische Eigenschaften des Teilchens darstellt.
eine Invariante, die
mechanische Eigenschaften des Teilchens darstellt.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_j^k = (m_0 c) \ \delta_j^k \quad \ \quad \ $}$](IMG283.GIF) |
|
|
(4.45) |
Analog zu der Impulstheorie lauten die Komponenten des Wirkungsintegrals in
der Energietheorie:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}s_k^1 = P_1^k \ \displaystyle\int \l...
...\quad = \quad
P_1^k \ \displaystyle\int \limits_{x^i} dx^{1k} \ . \ V^{kj} \ $}$](IMG284.GIF) |
|
|
(4.46) |
oder in der einfacheren Form geschrieben
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-s = m_0 c \ \displaystyle\int \limits^{l_2}_{l_1} cdt \ \sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}\ $}$](IMG285.GIF) |
|
|
(4.47) |
Analog können wir auch hier die Größenordnung der Wirkungsinvariante
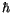 abschätzen. Dazu errechnen wir zuerst den Integrand in (4.46) aus. Für den
Viererwirkungsintegral erhalten wir:
abschätzen. Dazu errechnen wir zuerst den Integrand in (4.46) aus. Für den
Viererwirkungsintegral erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-s = \displaystyle\int \limits_{c {\...
...\ \ m = \displaystyle\frac {m_0}{\sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}}$](IMG286.GIF) |
|
|
(4.48) |
Mit (4.15) und
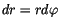 schreiben wir die beiden Terme in (4.48)
um und erhalten analog zu IT:
schreiben wir die beiden Terme in (4.48)
um und erhalten analog zu IT:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-s = -\displaystyle\frac {1}{2\pi}\l...
...\int \limits_{\phi_1=0}^{\phi_2=2\pi} \{ m v \ rd\varphi \} \ \right) \qquad $}$](IMG288.GIF) |
|
|
(4.49) |
Analog gilt die Gleichheit des dualen Abstands und folglich die Invarianz
der dualen Wirkungsintegrale.
Wir erhalten nach der Integration der Gleichung (4.49) schließlich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}s \ = \ \Big( \ -\displaystyle\frac ...
... \, m v \ r \, \} \ \ \ mit \ \ \ \lambda \equiv 2 \pi l \ \ \ oder \ \ ...\ $}$](IMG289.GIF) |
|
|
(4.50) |
Analog zu IT liefert das zeitabhängige Glied mit 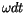 den
Term mit der
Welleneigenschaft. Der zweite Term wiedergibt den
Drehimpuls der ET.
den
Term mit der
Welleneigenschaft. Der zweite Term wiedergibt den
Drehimpuls der ET.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}s \ \geq \ \left(\, -\hbar \ + \ k\hbar\right) \quad \mbox{mit} \quad \ s=S \quad \ \ $}$](IMG291.GIF) |
|
|
(4.51) |
Wie wir später sehen werden, ist der Faktor
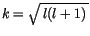 , wobei
, wobei
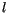 als sogennante Neben-Quantenzahl bezeichnet wird.
Für ein freies Teilchens
als sogennante Neben-Quantenzahl bezeichnet wird.
Für ein freies Teilchens 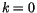 verschwindet die
Wirkung nicht und sie ist im Gegensatz zu IT von Null verschieden.
Dagegen aber für ein gebundenes Teilchen ist
verschwindet die
Wirkung nicht und sie ist im Gegensatz zu IT von Null verschieden.
Dagegen aber für ein gebundenes Teilchen ist
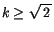 .
Folglich können wir für den ersten Term, die Compton Welle
schreiben:
.
Folglich können wir für den ersten Term, die Compton Welle
schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\, \hbar \ \leq \ \left( \displaysty...
...m c \ \Lambda \ }{2\pi} \right) \ \quad \mbox{\bf die Compton-Welle} \ \quad $}$](IMG296.GIF) |
|
|
(4.52) |
und für den zweiten Summand des Drehimpulsquants
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}k\, \hbar \ \leq \ \{ \ m v \ r \ \} \quad \ \mbox{\bf der \ Drehimpuls-Quant} \quad $}$](IMG297.GIF) |
|
|
(4.53) |





Nächste Seite: Das Variationsprinzip der Energietheorie
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Der Viererimpuls der Energietheorie
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_j^k = (m_0 c) \ \delta_j^k \quad \ \quad \ $}$](IMG283.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_j^k = (m_0 c) \ \delta_j^k \quad \ \quad \ $}$](IMG283.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}s_k^1 = P_1^k \ \displaystyle\int \l...
...\quad = \quad
P_1^k \ \displaystyle\int \limits_{x^i} dx^{1k} \ . \ V^{kj} \ $}$](IMG284.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-s = m_0 c \ \displaystyle\int \limits^{l_2}_{l_1} cdt \ \sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}\ $}$](IMG285.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-s = \displaystyle\int \limits_{c {\...
...\ \ m = \displaystyle\frac {m_0}{\sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}}$](IMG286.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-s = -\displaystyle\frac {1}{2\pi}\l...
...\int \limits_{\phi_1=0}^{\phi_2=2\pi} \{ m v \ rd\varphi \} \ \right) \qquad $}$](IMG288.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}s \ = \ \Big( \ -\displaystyle\frac ...
... \, m v \ r \, \} \ \ \ mit \ \ \ \lambda \equiv 2 \pi l \ \ \ oder \ \ ...\ $}$](IMG289.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}s \ \geq \ \left(\, -\hbar \ + \ k\hbar\right) \quad \mbox{mit} \quad \ s=S \quad \ \ $}$](IMG291.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\, \hbar \ \leq \ \left( \displaysty...
...m c \ \Lambda \ }{2\pi} \right) \ \quad \mbox{\bf die Compton-Welle} \ \quad $}$](IMG296.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}k\, \hbar \ \leq \ \{ \ m v \ r \ \} \quad \ \mbox{\bf der \ Drehimpuls-Quant} \quad $}$](IMG297.GIF)