



Nächste Seite: Die Wirkung in der
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Das Variationsprinzip der Impulstheorie
Inhalt
Index
Die Verbindungskurven zwischen zwei Punkten 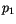 und
und 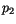 bestimmen wir
derart, daß zu zwei unterschiedlichen Ankunftszeiten
bestimmen wir
derart, daß zu zwei unterschiedlichen Ankunftszeiten 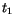 und
und 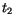 eines
Lichtsignals,
die auf dieser Kurve liegen, minimal wird. Analog zur Impulstheorie haben
wir für das Quadrat des infinitesimalen Viererortsvektors der Energietheorie:
eines
Lichtsignals,
die auf dieser Kurve liegen, minimal wird. Analog zur Impulstheorie haben
wir für das Quadrat des infinitesimalen Viererortsvektors der Energietheorie:
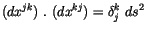 |
|
|
(4.35) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(V^{jk}) \ . \ (dx^{kj}) = \delta_j^k \ ds \ \ \ \ \ mit \ \ \ V^{1k} = \displaystyle\frac {dx^{1k}}{ds} \ \ $}$](IMG269.GIF) |
|
|
(4.36) |
In der Energietheorie bilden wir aus dem Skalaren (4.36) und dem
Teilchen spezifischen Vierertensor 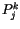 den Integrand des
Viererwirkungsintegrals. Analog zu der Impulstheorie
finden wir die Dimension
den Integrand des
Viererwirkungsintegrals. Analog zu der Impulstheorie
finden wir die Dimension
![$\bf [joule \ sec]$](IMG198.GIF) vor. Bezeichnen wir die Komponente
des Viererwirkungstensors mit
vor. Bezeichnen wir die Komponente
des Viererwirkungstensors mit 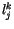 so können wir für seine Differentiale
schreiben:
so können wir für seine Differentiale
schreiben:
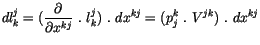 |
|
|
(4.37) |
Vergleichen wir die Klammer auf beiden Seiten, so finden wir :
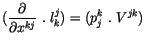 |
|
|
(4.38) |
Für seine Komponenten erhalten wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{\partial x^{k1}}\ l_k^1 = ( P \ \ , \ \ i\vec{p} ) \ \ $}$](IMG273.GIF) |
|
|
(4.39) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}mit \ \ \ P = \displaystyle\frac {(m...
...e\frac {( m_0 \ \vec{v})}{\sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}} \ \ $}$](IMG274.GIF) |
|
|
(4.40) |
Analog zu der Impulstheorie lässt sich das Dilemma der rechten
Seite von (4.39) beheben,
falls man sie als
Viererimpulsoperator auffasst. Das Produkt der Wirkungsinvariante
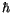 mit dem Vierergradient der ET wird als Viererimpuls bezeichnet.
mit dem Vierergradient der ET wird als Viererimpuls bezeichnet.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar_k^1 \displaystyle\frac {\partial}{\partial x^{k1}}= p^j \ \ \ mit \ \ \ \hbar_k^1 = \delta_k^1 \ \hbar \ \ $}$](IMG275.GIF) |
|
|
(4.41) |
Vergleicht man die beiden Seiten von (4.39) mit
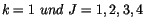 , so findet man:
, so findet man:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar\displaystyle\frac {\partial}{...
...tial}{\partial y}, \ \displaystyle\frac {\partial}{\partial z}) = i\vec{p} \ $}$](IMG276.GIF) |
|
|
(4.42) |
Analog gilt hier die Behauptung : das Quadrat des Viererimpulses ist eine
Invariante. Als Beweis quadrieren wir die Gleichung (4.41) und erhalten:
Für die rechte Seite dieser Gleichung gilt :
Diese Formel ist unter der relativistischen Hamilton Funktion
bekannt. Man findet oft die Schreibweise:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varepsilon^2 \ = \ c^2 p^2\ + \ (m_0c^2)^2 \ \ \ $}$](IMG278.GIF) |
|
|
(4.43) |
Man kann sie auch als linearisierte Form schreiben :
mit der kinetischen Energie
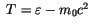 erhält man :
erhält man :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}T \ = \ \displaystyle\frac { m v^2}{ (1 + \displaystyle\frac {m_0}{m})} \ \ \ $}$](IMG281.GIF) |
|
|
(4.44) |
Für 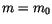 findet man die makroskopische kinetische Energie.
findet man die makroskopische kinetische Energie.




Nächste Seite: Die Wirkung in der
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Das Variationsprinzip der Impulstheorie
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(V^{jk}) \ . \ (dx^{kj}) = \delta_j^k \ ds \ \ \ \ \ mit \ \ \ V^{1k} = \displaystyle\frac {dx^{1k}}{ds} \ \ $}$](IMG269.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{\partial x^{k1}}\ l_k^1 = ( P \ \ , \ \ i\vec{p} ) \ \ $}$](IMG273.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}mit \ \ \ P = \displaystyle\frac {(m...
...e\frac {( m_0 \ \vec{v})}{\sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}} \ \ $}$](IMG274.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\hbar_k^1 \displaystyle\frac {\partial}{\partial x^{k1}}= p^j \ \ \ mit \ \ \ \hbar_k^1 = \delta_k^1 \ \hbar \ \ $}$](IMG275.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\hbar\displaystyle\frac {\partial}{...
...tial}{\partial y}, \ \displaystyle\frac {\partial}{\partial z}) = i\vec{p} \ $}$](IMG276.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P^2 \ - \ p^2 \ = \ m_0^2 c^2 \ \ $}$](IMG211.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varepsilon^2 \ = \ c^2 p^2\ + \ (m_0c^2)^2 \ \ \ $}$](IMG278.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}T \ = \ \displaystyle\frac { m v^2}{ (1 + \displaystyle\frac {m_0}{m})} \ \ \ $}$](IMG281.GIF)