




Nächste Seite: Die Wirkung in einem
Aufwärts: Die makroskopische Physik
Vorherige Seite: Das mechanische Viererpotential
Inhalt
Index
Der Kern der dualen Physik basiert auf Gleichheit des dualen Abstands,
die man unmittelbar auf Gleichheit der dualen Masse zurückführen kann.
Für das Quadrat des dualen Viererimpuls gilt:
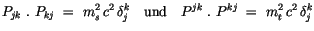 |
|
|
(14.10) |
Die Komponenten der linken Seiten dieser beiden Gleichungen lauten:
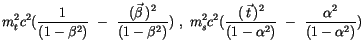 |
|
|
(14.11) |
Im Vergleich der ersten beiden Terme und mit der Auswahl des positiven
Vorzeichens finden wir:
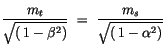 |
|
|
(14.12) |
Mit
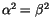 folgt schließlich:
folgt schließlich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m_0^t \ = \ m_0^s \quad , \quad \mbox{\bf tr\uml {a}ge Masse \ = \ schwere Masse} \qquad $}$](IMG965.GIF) |
|
|
(14.13) |
Schreiben wir
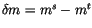 für die duale Teichenmasse, so können wir
sie Graphisch darstellen.
für die duale Teichenmasse, so können wir
sie Graphisch darstellen.
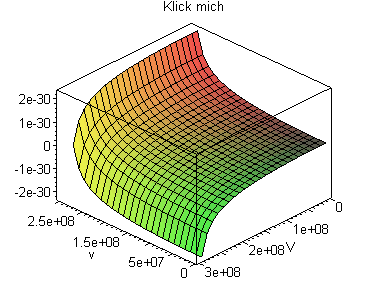
Übereinstimmend mit dem Eötvös-Dicke Experiment.





Nächste Seite: Die Wirkung in einem
Aufwärts: Die makroskopische Physik
Vorherige Seite: Das mechanische Viererpotential
Inhalt
Index
root
1999-07-07
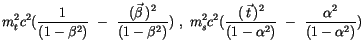
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m_0^t \ = \ m_0^s \quad , \quad \mbox{\bf tr\uml {a}ge Masse \ = \ schwere Masse} \qquad $}$](IMG965.GIF)