




Nächste Seite: Index
Aufwärts: Die makroskopische Physik
Vorherige Seite: Das Äquivalenzprinzip
Inhalt
Index
Für den Abstand eines beliebigen Bezugssystems des Makrokosmos schreiben wir
gemäß (2.32):
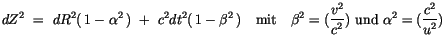 |
|
|
(14.14) |
Nun lautet das Wirkungsintegral eines beliebigen Bezugssystems mit (4.10), (4.46),
(5.20), (5.22)
Die Variation dieser Gleichung liefert gemäss unserer Förderung
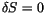 die Bewegungsgleichung unseres Problems. Wie schon bei (4.30)
bzw. (4.62) finden wir auch hier mit
die Bewegungsgleichung unseres Problems. Wie schon bei (4.30)
bzw. (4.62) finden wir auch hier mit
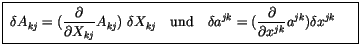 |
|
|
(14.16) |
nach Ausführung der partiellen Integration:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\cdots - \displaystyle\int \limits (...
...} + V^{k1} \, m \, {a^\prime}^{kj}\, )ds \ (\delta X_{jk} + \delta x^{kj}) \ $}$](IMG973.GIF) |
|
|
(14.17) |
Da der gasammte Ausdruck verschwinden wird, muß der Integrand ebenfalls
verschwinden.
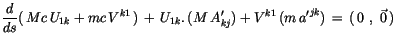 |
|
|
(14.18) |
Für die bessere Veranschaulichung der Gleichung (14.18) betrachten wir zuerst
die Terme der IT und vernachlässigen dabei seine imaginären Glieder.
Weiterhin setzen wir für die Vektoren 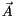 und
und 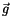
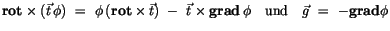 |
|
|
(14.19) |
die entsprechenden Ausdrücke ein, so ergibt sich, falls man die Limits aller
um die Sonne umkreisenden Planetenmassen gleich der Sonnenmasse setzt
(
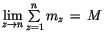 ):
):
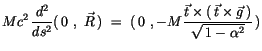 |
|
|
(14.20) |
Bei der Differenzierung der linken Seite halten wir die 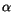 Koeffizienten
(2.66) Konstant
und in der rechten Seite berücksichtigen wir den
rechten Winkel (
Koeffizienten
(2.66) Konstant
und in der rechten Seite berücksichtigen wir den
rechten Winkel (
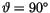 ) des Skalarprodukts
) des Skalarprodukts
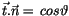 (2.67), so finden wir:
(2.67), so finden wir:
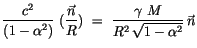 |
|
|
(14.21) |
Mit der Erkenntnis, daß die konstanten Terme die Bewegungsgleichungen nicht
beeinflußen, erhalten wir für 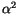 (
(
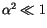 )
)
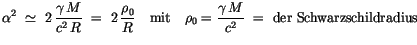 |
|
|
(14.22) |
Dabei gehen wir von den Tatsachen aus, daß die makroskopische
Prozesse viel langsamer als die mikroskopischen vorgehen.
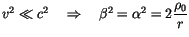 |
|
|
(14.23) |
Das Produkt der dualen Geschwindigkeiten der Materiewellen 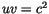 geht in
imaginären
geht in
imaginären 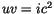 über. Diese Tatsache ist auf die reelle Raum-Zeit-Metrik
der Sonne (jedes Planeten) zurückzuführen. Demnach ist der Abstand eines
beliebigen Bezugssystems der Makrophysik im Gegensatz zu (14.14) durch die
Beziehung
über. Diese Tatsache ist auf die reelle Raum-Zeit-Metrik
der Sonne (jedes Planeten) zurückzuführen. Demnach ist der Abstand eines
beliebigen Bezugssystems der Makrophysik im Gegensatz zu (14.14) durch die
Beziehung
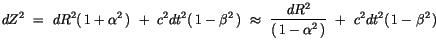 |
|
|
(14.24) |
gegeben. Für die Planetenbahnen um die Sonne geht
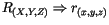 über
und wegen (14.23) gilt:
über
und wegen (14.23) gilt:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ^2 \ = \ \displaystyle\frac {dr_{(...
...\,)} \ + \ c^2 dt^2(\, 1 - 2\, \displaystyle\frac {\rho_0}{r}\,) \quad \quad $}$](IMG989.GIF) |
|
|
(14.25) |
Es ist erstaunlich, daß der Abstand (infinitesimales Linienelement) eines
beliebigen Bezugssystem aus der Steinzeit-Physik mit seinen undurchschaubaren
mathematischen Ansätzen und primitiven Modelvorstellungen des Kosmos diesem der
dualen Physik übereinstimmt. In Kugelkoordinaten ist diese
Gleichung mit radialen Kontration:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ^2 \ = \ \displaystyle\frac {dr^2}...
...hi^2 \ + \ c^2 dt^2(\, 1 - 2\, \displaystyle\frac {\rho_0}{r}\,) \quad \quad $}$](IMG990.GIF) |
|
|
(14.26) |
Aus dieser Beziehung kann man offenbar die Bewegungsgleichung der Planeten ableiten
und somit aus der Beobachtung herausgefundener Problematik unseres Sonnensystems,
wie die Rotverschiebung der Spektrallinien und die Lichtablenkung oder die
Prihelverschiebung, abhandeln.
Wir leiten nun zum Schluß die Gesetze des freien Falls ab. Im Gegensatz zur
Impuls-Theorie basiert die Energie-Theorie
auf der Existenz der kompromierten Materie im engsten Raum.
Die ET-Terme in (14.18) lauten:
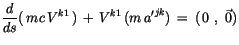 |
|
|
(14.27) |
Die runde Klammer im Zweiten Term vereinfachen wir bis auf den Ausdruck
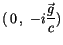 und finden für den zweiten Term:
und finden für den zweiten Term:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, \displaystyle\frac {\vec{\...
...yle\frac {\vec{\beta} \times \vec{g}}{c\sqrt{1-\beta^2}}\, \right] \right) \ $}$](IMG993.GIF) |
|
|
(14.28) |
Für die imaginären Glieder in (14.27) erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {d\vec{v}}{cdt\sq...
...\rule[-4mm]{0cm}{1cm}g\, = \, \gamma \, \displaystyle\frac {M_E}{r_E^2}\quad $}$](IMG994.GIF) |
|
|
(14.29) |
Nach Separation der Differentialkoeffizient und Integration dieser Gleichung finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}arcsin\beta\, - \, arcsin\beta_0 \, = \, -\displaystyle\frac {g\, t}{c}\quad $}$](IMG995.GIF) |
|
|
(14.30) |
Für die linke Seite gilt:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}arcsin\beta - arcsin\beta_0 \, = \, arcsin(\beta\sqrt{1-\beta^2_0}-\beta_0\sqrt{1-\beta^2})\quad $}$](IMG996.GIF) |
|
|
(14.31) |
Mit Rücksicht auf
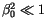 und
und 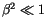 können wir schreiben:
können wir schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}arcsin\beta - arcsin\beta_0 \, \approx \, arcsin(\beta-\beta_0)\quad $}$](IMG999.GIF) |
|
|
(14.32) |
Letztlich erhalten wir für 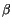 :
:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {v}{c})\, = \, - sin(\displaystyle\frac {g\, t}{c}) \, + \, (\displaystyle\frac {v_0}{c}) \quad $}$](IMG1001.GIF) |
|
|
(14.33) |
Wir berücksichtigen den langsamen Prozess-Ablauf der Makro-Systeme gegenüber
der Mikro-Physik
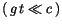 also für kleine
also für kleine 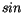 -Werte
-Werte
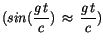 . Allgemein findet man
folgende drei Beziehungen:
. Allgemein findet man
folgende drei Beziehungen:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ddot{r}\ \, = \, -g \quad \quad$}$](IMG1005.GIF) |
|
|
(14.34) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\dot{r}\, = \, -g\, t \, + \, v_0 \quad \quad $}$](IMG1006.GIF) |
|
|
(14.35) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r \, = \, -\displaystyle\frac {1}{\, 2 \, }\, g\, t^2 \, + \, v_0\, t \, + \, r_0 \quad $}$](IMG1007.GIF) |
|
|
(14.36) |
Die Abhandlung der makroskopischen Physik ist nicht das Zielthema unserer
Darlegungen gewesen, außerdem würde sie den Rahmen dieses Buches
sprengen.
Wir schließen nun mit mahnenden Worten:
Leider ist unser Planet durch die angewandten Naturwissenschaften
weitgehend zerstört. Denken vor Handeln hätte das Schlimmste verhindert,
aber das Vorausdenken ist nie die Stärke der Menschen gewesen.





Nächste Seite: Index
Aufwärts: Die makroskopische Physik
Vorherige Seite: Das Äquivalenzprinzip
Inhalt
Index
root
1999-07-07
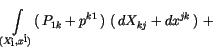
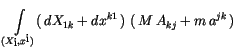
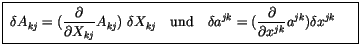
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\cdots - \displaystyle\int \limits (...
...} + V^{k1} \, m \, {a^\prime}^{kj}\, )ds \ (\delta X_{jk} + \delta x^{kj}) \ $}$](IMG973.GIF)
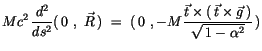
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ^2 \ = \ \displaystyle\frac {dr_{(...
...\,)} \ + \ c^2 dt^2(\, 1 - 2\, \displaystyle\frac {\rho_0}{r}\,) \quad \quad $}$](IMG989.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ^2 \ = \ \displaystyle\frac {dr^2}...
...hi^2 \ + \ c^2 dt^2(\, 1 - 2\, \displaystyle\frac {\rho_0}{r}\,) \quad \quad $}$](IMG990.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, \displaystyle\frac {\vec{\...
...yle\frac {\vec{\beta} \times \vec{g}}{c\sqrt{1-\beta^2}}\, \right] \right) \ $}$](IMG993.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {d\vec{v}}{cdt\sq...
...\rule[-4mm]{0cm}{1cm}g\, = \, \gamma \, \displaystyle\frac {M_E}{r_E^2}\quad $}$](IMG994.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}arcsin\beta\, - \, arcsin\beta_0 \, = \, -\displaystyle\frac {g\, t}{c}\quad $}$](IMG995.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}arcsin\beta - arcsin\beta_0 \, = \, arcsin(\beta\sqrt{1-\beta^2_0}-\beta_0\sqrt{1-\beta^2})\quad $}$](IMG996.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}arcsin\beta - arcsin\beta_0 \, \approx \, arcsin(\beta-\beta_0)\quad $}$](IMG999.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {v}{c})\, = \, - sin(\displaystyle\frac {g\, t}{c}) \, + \, (\displaystyle\frac {v_0}{c}) \quad $}$](IMG1001.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ddot{r}\ \, = \, -g \quad \quad$}$](IMG1005.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\dot{r}\, = \, -g\, t \, + \, v_0 \quad \quad $}$](IMG1006.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}r \, = \, -\displaystyle\frac {1}{\, 2 \, }\, g\, t^2 \, + \, v_0\, t \, + \, r_0 \quad $}$](IMG1007.GIF)