




Nächste Seite: Das Äquivalenzprinzip
Aufwärts: Die makroskopische Physik
Vorherige Seite: Die makroskopische Physik
Inhalt
Index
Das massenabhängige Teilchenpotential charakterisiert das mechanische
Potential. Nach Newtonscher Theorie ist das skalare Potential, das sogenannte
Gravitationspotential, die einzige
Wechselwirkungsursache im Universum.
Gehen wir davon aus, daß keine bevorzugten Planetenbahnen existieren, so
würde jeder Planet in einer beliebigen Ebene auf seiner Bahn um die Sonne
kreisen.
Daraus lässt sich schlußfolgern, daß die Gestalt
eines Sonnensystems auch nach den Gesetzen der Wahrscheinlichkeitstheorie in
seltenen Fällen eine ebene
Struktur aufweist, ganz im Gegenteil, sie wird eher eine Ellipsoide-Struktur
besitzen, was aber im allgemeinen den Tatsachen widerspricht.
Die Planeten unseres Sonnensystems bevorzugen stets eine Ebene, um so die Sonne
zu umkreisen. Dieser Umstand ist auf das quasi Konstante, durch die
Sonnenrotation entstandene Feld, das diese Ebene Senkrecht durchquert,
zurückzuführen. Dieses Feld ist das sogenannte Gravitationsvirbelfeld
,
das für die Entstehung der Asteroiden bzw. Saturn-Ringe verantwortlich ist.
Analog zu elektromagnetischen Viererpotential bilden skalare
und das Vektorpotential die Komponenten dieses Vierervektors.
In der IT ist diese Beziehung gleich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_j \ = \ ( \ i\phi \ , \ \ \display...
...\displaystyle\frac {kg}{m} \ \quad \mbox{\bf Das Viererpotential der IT} \ \ $}$](IMG946.GIF) |
|
|
(14.1) |
Die skalare Komponente stellt das imaginäre Skalarpotential der ET dar.
Dagegen ist die Vektorkomponente das reelle Vektorpotential der IT.
Die Dimension dieses Vierervektors wurde mit
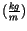 festgelegt.
Analog zu der IT können wir das Viererpotential der Energietheorie
angeben:
festgelegt.
Analog zu der IT können wir das Viererpotential der Energietheorie
angeben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}a^j \ = \ ( \ \displaystyle\frac {\v...
...\ \displaystyle\frac {m}{s} \ \quad \mbox{\bf Das Viererpotential de ET} \ \ $}$](IMG948.GIF) |
|
|
(14.2) |
Das Viererpotential der ET weist eine andere Dimension auf, die mit
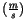 bezeichnet wird. Die in (14.2) enthaltene Proportionalitätsfaktor
bezeichnet wird. Die in (14.2) enthaltene Proportionalitätsfaktor
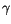 wird die Gravitationskonstante
ganannt.
wird die Gravitationskonstante
ganannt.
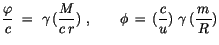 |
|
|
(14.3) |
Analog zur Kapittel 5 (s.S.41) gelten folgende Beziehungen:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\gamma \, }{ \, ...
...d \kappa^{-1}\, = \, 1.347459416\ \ 10^{27} \,\displaystyle\frac {kg\,}{m} \ $}$](IMG952.GIF) |
|
|
(14.4) |
Wobei 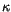 die Gravitationswirbelkonstante ist. Wir errechnen zunächst die
mechanische Feinstrukturkonstante des Wasserstoffatoms, um die Größenordnung
der mechanischen Wechselwirkung abzuschätzen.
die Gravitationswirbelkonstante ist. Wir errechnen zunächst die
mechanische Feinstrukturkonstante des Wasserstoffatoms, um die Größenordnung
der mechanischen Wechselwirkung abzuschätzen.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\alpha_m \ = \ \gamma\, (\displaystyle\frac {\, m_e \, m_p}{c\,\hbar}) \ = \ 3.214446 \ \ 10^{-42}\quad $}$](IMG953.GIF) |
|
|
(14.5) |
oder als Quotient erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {\alpha_m\, }{\alpha_f\, }) \, = \ 4,4056 \ \ 10^{-40} \ \quad $}$](IMG954.GIF) |
|
|
(14.6) |
Bei dieser Größenordnung werden wir auf die Abhandlung
der mikroskopischen Feldtheorie verzichten und uns mit der Grenzfrage der
makroskopischen Physik befassen.
Der Makrozustand ist der Übergang der Dreiquanten
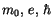
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lim\limits_{n\to\infty} \ m_0 \ \sum\limits_{Z=1}^{n} Z \ = \ M \ = \ kg \quad $}$](IMG956.GIF) |
|
|
(14.7) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lim\limits_{n\to\infty} \ e \ \sum\limits_{Z=1}^{n} Z \ = \ Q \ = \ As \quad $}$](IMG957.GIF) |
|
|
(14.8) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lim\limits_{n\to\infty} \ \hbar \ \sum\limits_{j=\frac{1}{2}}^{n} j \ = \ L \ = \ VAs^2 \quad $}$](IMG958.GIF) |
|
|
(14.9) |
in den Größen 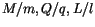 . Diese sind charakteristisch für die
kontinuierlichen Zustände in der dualen Physik. Mit den kontinuierlichen
Zuständen meinen wir, die nichtdiskreten Zustände.
. Diese sind charakteristisch für die
kontinuierlichen Zustände in der dualen Physik. Mit den kontinuierlichen
Zuständen meinen wir, die nichtdiskreten Zustände.





Nächste Seite: Das Äquivalenzprinzip
Aufwärts: Die makroskopische Physik
Vorherige Seite: Die makroskopische Physik
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_j \ = \ ( \ i\phi \ , \ \ \display...
...\displaystyle\frac {kg}{m} \ \quad \mbox{\bf Das Viererpotential der IT} \ \ $}$](IMG946.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}A_j \ = \ ( \ i\phi \ , \ \ \display...
...\displaystyle\frac {kg}{m} \ \quad \mbox{\bf Das Viererpotential der IT} \ \ $}$](IMG946.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}a^j \ = \ ( \ \displaystyle\frac {\v...
...\ \displaystyle\frac {m}{s} \ \quad \mbox{\bf Das Viererpotential de ET} \ \ $}$](IMG948.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\gamma \, }{ \, ...
...d \kappa^{-1}\, = \, 1.347459416\ \ 10^{27} \,\displaystyle\frac {kg\,}{m} \ $}$](IMG952.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\alpha_m \ = \ \gamma\, (\displaystyle\frac {\, m_e \, m_p}{c\,\hbar}) \ = \ 3.214446 \ \ 10^{-42}\quad $}$](IMG953.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {\alpha_m\, }{\alpha_f\, }) \, = \ 4,4056 \ \ 10^{-40} \ \quad $}$](IMG954.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lim\limits_{n\to\infty} \ m_0 \ \sum\limits_{Z=1}^{n} Z \ = \ M \ = \ kg \quad $}$](IMG956.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lim\limits_{n\to\infty} \ e \ \sum\limits_{Z=1}^{n} Z \ = \ Q \ = \ As \quad $}$](IMG957.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\lim\limits_{n\to\infty} \ \hbar \ \sum\limits_{j=\frac{1}{2}}^{n} j \ = \ L \ = \ VAs^2 \quad $}$](IMG958.GIF)