




Nächste Seite: Die Eigenwerte der Impulstheorie
Aufwärts: Das magnetische Moment
Vorherige Seite: Das magnetische Moment der
Inhalt
Index
Analog zu der IT bilden wir das Integral des magnetischen Moments
ET aus Invarianten 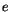 ,
, 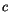 und
und 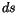 :
:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-m^{1k} \ = \ (\displaystyle\frac {\, e^-\, }{m_0})\, m_0\, c \displaystyle\int \limits dx^{1k} \ . \ V^{kj} \quad $}$](IMG545.GIF) |
|
|
(8.10) |
Diese Gleichung ist bis auf den Faktor
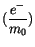 dem Wirkungsintegral
(4.61) identisch. Analog variieren wir diese Gleichung und nach partieller Integration
finden wir:
dem Wirkungsintegral
(4.61) identisch. Analog variieren wir diese Gleichung und nach partieller Integration
finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta m^{1k} \ = \ (\displaystyle\...
...delta x^{1k} \ . \ \displaystyle\frac {\, d\, }{ds}(\, P^{kj}\, )\, ds \quad $}$](IMG546.GIF) |
|
|
(8.11) |
Aus Analogie zu dem Drehimpuls können wir für den magnetischen Moment,
den wir hier mit 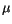 bezeichnen schreiben:
bezeichnen schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\mu \partial^{1k}\ = \ (\displaysty...
...eft( (\displaystyle\frac {\, e^-\, }{m_0}) \ \hbar\right) \partial^{1k}\quad $}$](IMG547.GIF) |
|
|
(8.12) |
Für die Invariante 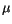 des magnetischen Momentes finden wir:
des magnetischen Momentes finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu \ = \ (\, \displaystyle\frac {\, e^-\, }{m_0}\, ) \, \hbar \quad \quad \quad $}$](IMG526.GIF) |
|
|
(8.13) |
Der erste Term in (8.11) ist analog zu der IT die Vierertensorskomponente
des magnetischen Moments der ET:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m^{1k} \ = \ x^{1k} \ . \ \mu \partial^{jk}\quad \quad $}$](IMG548.GIF) |
|
|
(8.14) |
Errechnen wir seine Komponenten, so erhalten wir:
und nach Ausrechnung des skalaren Terms finden wir die einfachere Schreibweise
bei konstantem Radius:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m^{1k} \ = \ \left(\, \mu\, \ , \ -i...
...f grad} \, ct \, + \, \mu (\, \vec{r} \times {\sf grad}\, ) \, \right) \quad $}$](IMG550.GIF) |
|
|
(8.15) |
An dieser Stelle ist es angebracht zu erwähnen, daß die Gleichungen (8.6) und
(8.15) bis auf das Vorzeichen die gleichen Strukturen aufweisen. Die reellen
Vektorkomponenten der beiden magnetischen Momente sind entgegengerichtet.
Der letzte Term in der runden Klammer ist der Vektor des axialen magnetischen
Moments.
Der Betrag dieses Vektorprodukts ist analog zu IT:
Der letzte Term ist eine
Konstante
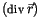 und trägt nur zur Nullpunktverschiebung bei.
Bezeichnen wir mit
und trägt nur zur Nullpunktverschiebung bei.
Bezeichnen wir mit
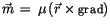 , so lauten
seine Eigenwerte analog zu IT:
, so lauten
seine Eigenwerte analog zu IT:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m \, = \, \sqrt{\, l(l+1)\, }\, \mu \quad \quad $}$](IMG554.GIF) |
|
|
(8.16) |
Wir schreiben 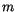 mit
mit
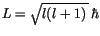 und dem sogenannten g-Faktor
um und berücksichtigen wir, daß für Elektron
und dem sogenannten g-Faktor
um und berücksichtigen wir, daß für Elektron 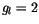 beträgt, so finden wir:
beträgt, so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m \, = \, g_l \, (\displaystyle\frac {e^-}{2 \, m_0}) \ L \quad \quad $}$](IMG558.GIF) |
|
|
(8.17) |
Man bezeichnet sie auch mit 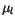 . Mit (8.8) das Bohr-Magneton
erhalten wir für
. Mit (8.8) das Bohr-Magneton
erhalten wir für 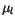 :
:
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\mu_l \, = \, g_l \, \mu_B \, \sqrt{l(l+1)} \, = \, g_l \, \mu_B\, (\displaystyle\frac {L}{\hbar}) \quad \quad $}$](IMG560.GIF) |
|
|
(8.18) |





Nächste Seite: Die Eigenwerte der Impulstheorie
Aufwärts: Das magnetische Moment
Vorherige Seite: Das magnetische Moment der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-m^{1k} \ = \ (\displaystyle\frac {\, e^-\, }{m_0})\, m_0\, c \displaystyle\int \limits dx^{1k} \ . \ V^{kj} \quad $}$](IMG545.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-m^{1k} \ = \ (\displaystyle\frac {\, e^-\, }{m_0})\, m_0\, c \displaystyle\int \limits dx^{1k} \ . \ V^{kj} \quad $}$](IMG545.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta m^{1k} \ = \ (\displaystyle\...
...delta x^{1k} \ . \ \displaystyle\frac {\, d\, }{ds}(\, P^{kj}\, )\, ds \quad $}$](IMG546.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\mu \partial^{1k}\ = \ (\displaysty...
...eft( (\displaystyle\frac {\, e^-\, }{m_0}) \ \hbar\right) \partial^{1k}\quad $}$](IMG547.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\mu \ = \ (\, \displaystyle\frac {\, e^-\, }{m_0}\, ) \, \hbar \quad \quad \quad $}$](IMG526.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m^{1k} \ = \ x^{1k} \ . \ \mu \partial^{jk}\quad \quad $}$](IMG548.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m^{1k} \ = \ \mu \left(\, (\, \displ...
...ial t}\vec{r}\, ) \, + \, (\, \vec{r} \times {\sf grad}\, ) \, \right) \quad $}$](IMG549.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m^{1k} \ = \ \left(\, \mu\, \ , \ -i...
...f grad} \, ct \, + \, \mu (\, \vec{r} \times {\sf grad}\, ) \, \right) \quad $}$](IMG550.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m \, = \, \sqrt{\, l(l+1)\, }\, \mu \quad \quad $}$](IMG554.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}m \, = \, g_l \, (\displaystyle\frac {e^-}{2 \, m_0}) \ L \quad \quad $}$](IMG558.GIF)
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\mu_l \, = \, g_l \, \mu_B \, \sqrt{l(l+1)} \, = \, g_l \, \mu_B\, (\displaystyle\frac {L}{\hbar}) \quad \quad $}$](IMG560.GIF)