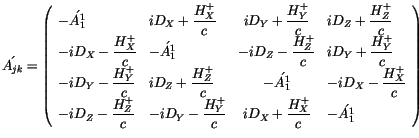Nächste Seite: Die 2. Teilchen-Gleichungen der
Aufwärts: Das Feld in der
Vorherige Seite: Das Feld in der
Inhalt
Index
In diesem Abschnitt werden wir die elektromagnetischen Gleichungen der
Impulstheorie behandeln.
Als typische IT-Teilchen bezeichnen wir Elementarteilchen mit
positiver Ladung. Zuerst
beschäftigen wir uns mit der zweiten Rundenklammer in (6.1) und werden diesem
Sachverhalt mit folgendem Ansatz nachgehen.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{jk}\ . \ ( \partial_{kj}\ . \ A_{kj} ) \ = \ \delta_j^k \partial_j^2 \ A_{kj} \qquad $}$](IMG383.GIF) |
|
|
(6.2) |
Für die Komponente der Rundenklammer in (6.2) benutzen wir untere Beziehung:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{k1}\ . \ A_{kj} \ = \ (\pa...
...}A_{1j} \ , \ \partial_{k1}\ . \ ( A_{2j} \ , \ A_{3j} \ , \ A_{4j} )) \quad $}$](IMG384.GIF) |
|
|
(6.3) |
und erhalten für die Komponenten des elektromagnetischen Viererfeldtensors:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}- \acute{A_1^1} \ = \ -( \ \displays...
...partial T}\phi^- \ + \ {\bf div}(\displaystyle\frac {\vec{A}^+}{c}) ) \qquad $}$](IMG385.GIF) |
|
|
(6.4) |
Der Term in der Klammer (6.4), die Viererdivergenz
ist ein Viererskalar und ihr wird keine physikalische Bedeutung beigemessen
6.2 .
.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}i\vec{D} = -i( \ \displaystyle\frac ...
... ) \ \ \mbox{mit} \ \ \vec{D} = \ ({\vec{D^-}}_{(R)} + {\vec{D^+}}_{(cT)}) \ $}$](IMG387.GIF) |
|
|
(6.5) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {\vec{H}^+}{c}) \ = \ {\bf rot} (\displaystyle\frac {\vec{A}^+}{c}) \qquad $}$](IMG388.GIF) |
|
|
(6.6) |
(6.5) und (6.6) sind charakteristik für die Vekortransformationen, die aus zwei
unterschiedlichen Vektortypen bestehen. Zum ersten zählt der imaginäre Vektor
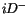 , der als dielektrische Verschiebung bezeichnet wird. Seine räumliche
Komponente, die aus der Anwendung des Gradientenvektors auf das skalaren Potential
(
, der als dielektrische Verschiebung bezeichnet wird. Seine räumliche
Komponente, die aus der Anwendung des Gradientenvektors auf das skalaren Potential
(
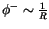 ) gewonnen wird, stellt ein gestärktes Gefälle
(
) gewonnen wird, stellt ein gestärktes Gefälle
(
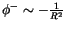 ) entgegengesetzter Richtung dar. Bei der zeitabhängigen
Komponete spricht man von zeitlicher Ableitung des Vektorpotentials. Zum zweiten
zählt der reelle Vektor (
) entgegengesetzter Richtung dar. Bei der zeitabhängigen
Komponete spricht man von zeitlicher Ableitung des Vektorpotentials. Zum zweiten
zählt der reelle Vektor (
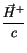 ), der senkrecht zu dem Gradientenvektor
), der senkrecht zu dem Gradientenvektor 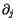 und dem Vektorpotential
und dem Vektorpotential 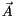 steht und die magnetische Feldstärke gennant
wird. Für die Komponenten des elektromagnetischen Feldtensors können wir schreiben :
steht und die magnetische Feldstärke gennant
wird. Für die Komponenten des elektromagnetischen Feldtensors können wir schreiben :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\acute{A_{1k}} \ = \ ( \ -\acute{A_1...
... i \vec{D} \ ) \ + \ ( \ 0 \ , \ (\displaystyle\frac {\vec{H}^+}{c}) \ ) \ $\ }$](IMG395.GIF) |
|
|
(6.7) |
In der dualen Physik ist jede Multiplikation mit dem Vierergradiententensor
eine afine Transformation. Aus dem ersten Term in (6.7) geht hervor, daß eine
Bezugssystemumwandlung stattgefunden hat. Der Pseudovierervektor aus ET
ist die Komponente des transponierten Pseudovierertensors6.3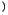 .
In zweiten Term ist die skalare Komponente des Vierervektors gleich null.
Wir sagen: der Vierervektor ist schief oder dessen Vierertensor hat eine schiefe
Matrix. Nun lautet die Matrix des gemischten Viererfeldtensors:
.
In zweiten Term ist die skalare Komponente des Vierervektors gleich null.
Wir sagen: der Vierervektor ist schief oder dessen Vierertensor hat eine schiefe
Matrix. Nun lautet die Matrix des gemischten Viererfeldtensors:
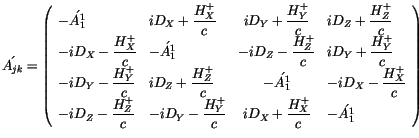 |
|
|
(6.8) |





Nächste Seite: Die 2. Teilchen-Gleichungen der
Aufwärts: Das Feld in der
Vorherige Seite: Das Feld in der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{jk}\ . \ ( \partial_{kj}\ . \ A_{kj} ) \ = \ \delta_j^k \partial_j^2 \ A_{kj} \qquad $}$](IMG383.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{jk}\ . \ ( \partial_{kj}\ . \ A_{kj} ) \ = \ \delta_j^k \partial_j^2 \ A_{kj} \qquad $}$](IMG383.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{k1}\ . \ A_{kj} \ = \ (\pa...
...}A_{1j} \ , \ \partial_{k1}\ . \ ( A_{2j} \ , \ A_{3j} \ , \ A_{4j} )) \quad $}$](IMG384.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}- \acute{A_1^1} \ = \ -( \ \displays...
...partial T}\phi^- \ + \ {\bf div}(\displaystyle\frac {\vec{A}^+}{c}) ) \qquad $}$](IMG385.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}i\vec{D} = -i( \ \displaystyle\frac ...
... ) \ \ \mbox{mit} \ \ \vec{D} = \ ({\vec{D^-}}_{(R)} + {\vec{D^+}}_{(cT)}) \ $}$](IMG387.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {\vec{H}^+}{c}) \ = \ {\bf rot} (\displaystyle\frac {\vec{A}^+}{c}) \qquad $}$](IMG388.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\acute{A_{1k}} \ = \ ( \ -\acute{A_1...
... i \vec{D} \ ) \ + \ ( \ 0 \ , \ (\displaystyle\frac {\vec{H}^+}{c}) \ ) \ $\ }$](IMG395.GIF)