




Nächste Seite: Die 3. Teilchen-Gleichungen der
Aufwärts: Das Feld in der
Vorherige Seite: Die 1. Teilchen-Gleichungen der
Inhalt
Index
Wir errechnen nun die linke Seite von (6.2) und vergleichen die Resultate
mit der rechten Seite. Für seine Komponente erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{1k}\ . \ \acute{A_{kj}} \ ...
...k} \ . \ ( \acute{A_{2j}} \ , \ \acute{A_{3j}} \ , \ \acute{A_{4j}} )) \quad $}$](IMG397.GIF) |
|
|
(6.9) |
Für die Viererdivergenz finden wir :
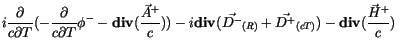 |
|
|
(6.10) |
Zunächst ordnen wir zur besseren Übersicht diese Beziehung um in zwei Gruppen. Die erste Gruppe
bleibt erhalten und sie ist ungleich null:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i((\displaystyle\frac {\partial}{c \partial T})^2 \phi^- + {\bf div}\vec{D^-}_{(R)}) \qquad $}$](IMG399.GIF) |
|
|
(6.11) |
In der zweiten Gruppe gleichen sich, jeweils der zweite Term in den runden Klammern in (6.10)
die div der zeitlichen Komponenten der dielektrischen
Verschiebung und die zeitliche Änderung des Skalars div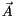 aus.
Übrig bleibt die physikaliche Aussage des letzten Gliedes div(
aus.
Übrig bleibt die physikaliche Aussage des letzten Gliedes div(
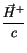 ),
die wir später abhandeln werden.
),
die wir später abhandeln werden.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i(\displaystyle\frac {\partial}{c \...
...frac {\vec{A}^+}{c})) - {\bf div}(\displaystyle\frac {\vec{H}^+}{c}) \ = 0 \ $}$](IMG400.GIF) |
|
|
(6.12) |
Für die Viererrotation erhalten wir :
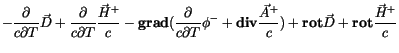 |
|
|
(6.13) |
Ähnlich wie bei der Viererdivergenz unterteilen wir die Glieder von (6.13) in
zwei Gruppen. Nach der Aufspaltung des Verschiebungsvektors kann man für das
erste und dritte Glied in (6.13) schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{c \par...
...f grad}\displaystyle\frac {\partial}{c \partial T}\phi^- \ = \ \vec{0} \quad $}$](IMG402.GIF) |
|
|
(6.14) |
Die zeitliche Änderung der dielektrischen Verschiebung ist der
Gradient der zeitlichen Änderung des Skalars 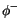 entgegengerichtet.
Einen weiteren Nullvektor erhalten wir aus dem zweiten und fünften Glied
in (6.13) :
entgegengerichtet.
Einen weiteren Nullvektor erhalten wir aus dem zweiten und fünften Glied
in (6.13) :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{c \par...
...partial}{c \partial T}\displaystyle\frac {\vec{A}^+}{c}) \ = \ \vec{0} \quad $}$](IMG404.GIF) |
|
|
(6.15) |
Die Beziehungen (6.12), (6.14) und (6.15) bilden die Komponenten des Nulltensors.
Unter der Vernachlässigung der runden Klammer in (6.12) und die (6.14) finden
wir für seine Komponente :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\Big( -{\bf div}(\displaystyle\frac ...
...e\frac {\vec{H}^+}{c}+ {\bf rot}\vec{D}) \Big) = ( \ 0 \ , \ \ \vec{0} \ ) \ $}$](IMG405.GIF) |
|
|
(6.16) |
Aus dem Prinzip des maximalen Aufwands (die geschloßene Feldlinien) schließen
wir, daß die magnetische Feldstärke 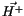 Quellfrei ist und daher die
Divergenz vom
Quellfrei ist und daher die
Divergenz vom 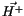 verschwindet. Außerdem verschwindet die Rotation des
Verschiebungsvektors
verschwindet. Außerdem verschwindet die Rotation des
Verschiebungsvektors
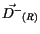 . Somit gilt als letztes:
. Somit gilt als letztes:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\bf rot \ grad} \ \phi^- \ = \ \vec{0} \ \qquad $}$](IMG408.GIF) |
|
|
(6.17) |
Mit (6.11) und der Restglieder in (6.13) lautet die Komponente dieses Tensors:
![$\displaystyle \fbox {$ \begin{array}{rcl}\rule[-4mm]{0cm}{1cm}\Big(-i(\displays...
... {\bf rot}(\displaystyle\frac {\vec{H}^+}{c})\Big) \end{array} \qquad \qquad $}$](IMG409.GIF) |
|
|
(6.18) |
Aus dem Vergleich mit der rechten Seite von (6.2) fnden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}- {\bf grad} \ (\, {\bf div}\display...
...A}^+}{c}\, ) \ = \ - {\bf grad}^2 (\displaystyle\frac {\vec{A}^+}{c}) \qquad $}$](IMG410.GIF) |
|
|
(6.19) |
Die Dimension von (6.18) wie man entnehmen kann, ist Ladung pro Volumen.
Sie wird daher als die Viererdichte bezeichnet.
Wir gehen grundsätzlich davon aus, daß von den Volumen eingeschloßene
Ladung elektrostatischen Ursprung hat. Um die üblichen Maxwellschen Gleichungen
zu erhalten, müßen wir die
Viererdivergenz (6.4) als Konstant annehmen. Folglich
verschwinden alle seine Ableitungen. Die Komponente dieses Nulltensors aus
(6.18) lautet:
![$\displaystyle \fbox {$ \rule[-4mm]{0cm}{1cm}\Big(-i(\displaystyle\frac {\partia...
...isplaystyle\frac {\vec{A}^+}{c})\Big) \ = \ (\, 0 \ , \ \ \vec{0}\, ) \qquad $}$](IMG411.GIF) |
|
|
(6.20) |
Führen wir die Bezeichnung 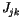 für das Tensor der Viererdichte ein und
unter der Berücksichtigung von (6.16) und (6.20) erhalten wir die berühmte Maxwellsche Gleichungen:
für das Tensor der Viererdichte ein und
unter der Berücksichtigung von (6.16) und (6.20) erhalten wir die berühmte Maxwellsche Gleichungen:
Diese Annahme wie man aus dem Vergleich mit der rechten Seite von (6.2) entnehmen
kann ist nicht zuläßig. Die vollständige Gleichung lautet:
![$\displaystyle \fbox {$ \rule[-4mm]{0cm}{1cm}J_{k1} = \Big(-i(\displaystyle\frac...
...ec{D^+}_{(cT)} - {\bf grad}^2 (\displaystyle\frac {\vec{A}^+}{c}\, )\Big) \, $}$](IMG414.GIF) |
|
|
(6.21) |
Für die symbolische Darstellung der Viererdichte schreiben wir vorerst:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}J_{k1} \ = \ \alpha ( \ -i{\varrho^-...
...vec{R})}\ , \ \ \displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c}\ ) \qquad $}$](IMG415.GIF) |
|
|
(6.22) |
Die von dem Volumen 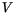 eingeschloßene Elementarladung
(
eingeschloßene Elementarladung
(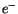 )
ist offenbar nach dem Gesetz (4.68) räumlich verteilt.
)
ist offenbar nach dem Gesetz (4.68) räumlich verteilt.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho^-_{(cT,\vec{R})} \ = \ {\var...
...\{ \displaystyle\frac { P \ cT \ - \ \vec{P} . \vec{R} }{\hbar} \right\} \ \ $}$](IMG417.GIF) |
|
|
(6.23) |
Analog finden wir für das positive Elementarteilchen (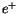 ) :
) :





Nächste Seite: Die 3. Teilchen-Gleichungen der
Aufwärts: Das Feld in der
Vorherige Seite: Die 1. Teilchen-Gleichungen der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{1k}\ . \ \acute{A_{kj}} \ ...
...k} \ . \ ( \acute{A_{2j}} \ , \ \acute{A_{3j}} \ , \ \acute{A_{4j}} )) \quad $}$](IMG397.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\partial_{1k}\ . \ \acute{A_{kj}} \ ...
...k} \ . \ ( \acute{A_{2j}} \ , \ \acute{A_{3j}} \ , \ \acute{A_{4j}} )) \quad $}$](IMG397.GIF)
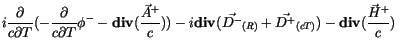
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i((\displaystyle\frac {\partial}{c \partial T})^2 \phi^- + {\bf div}\vec{D^-}_{(R)}) \qquad $}$](IMG399.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i(\displaystyle\frac {\partial}{c \...
...frac {\vec{A}^+}{c})) - {\bf div}(\displaystyle\frac {\vec{H}^+}{c}) \ = 0 \ $}$](IMG400.GIF)
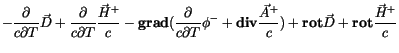
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{c \par...
...f grad}\displaystyle\frac {\partial}{c \partial T}\phi^- \ = \ \vec{0} \quad $}$](IMG402.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{c \par...
...partial}{c \partial T}\displaystyle\frac {\vec{A}^+}{c}) \ = \ \vec{0} \quad $}$](IMG404.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\Big( -{\bf div}(\displaystyle\frac ...
...e\frac {\vec{H}^+}{c}+ {\bf rot}\vec{D}) \Big) = ( \ 0 \ , \ \ \vec{0} \ ) \ $}$](IMG405.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}{\bf rot \ grad} \ \phi^- \ = \ \vec{0} \ \qquad $}$](IMG408.GIF)
![$\displaystyle \fbox {$ \begin{array}{rcl}\rule[-4mm]{0cm}{1cm}\Big(-i(\displays...
... {\bf rot}(\displaystyle\frac {\vec{H}^+}{c})\Big) \end{array} \qquad \qquad $}$](IMG409.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}- {\bf grad} \ (\, {\bf div}\display...
...A}^+}{c}\, ) \ = \ - {\bf grad}^2 (\displaystyle\frac {\vec{A}^+}{c}) \qquad $}$](IMG410.GIF)
![$\displaystyle \fbox {$ \rule[-4mm]{0cm}{1cm}\Big(-i(\displaystyle\frac {\partia...
...isplaystyle\frac {\vec{A}^+}{c})\Big) \ = \ (\, 0 \ , \ \ \vec{0}\, ) \qquad $}$](IMG411.GIF)
![$\displaystyle \fbox {$ \rule[-4mm]{0cm}{1cm}J_{k1} \ = \ \Big(-i{\bf div}\vec{D...
...T}\vec{D^+}_{(cT)} + {\bf rot} (\displaystyle\frac {\vec{H}^+}{c}\, )\Big) \ $}$](IMG413.GIF)
![$\displaystyle \fbox {$ \rule[-4mm]{0cm}{1cm}J_{k1} = \Big(-i(\displaystyle\frac...
...ec{D^+}_{(cT)} - {\bf grad}^2 (\displaystyle\frac {\vec{A}^+}{c}\, )\Big) \, $}$](IMG414.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}J_{k1} \ = \ \alpha ( \ -i{\varrho^-...
...vec{R})}\ , \ \ \displaystyle\frac {{\vec{J}^+}_{(cT,\vec{R})}}{c}\ ) \qquad $}$](IMG415.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho^-_{(cT,\vec{R})} \ = \ {\var...
...\{ \displaystyle\frac { P \ cT \ - \ \vec{P} . \vec{R} }{\hbar} \right\} \ \ $}$](IMG417.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho^+_{(cT,\vec{R})} \ = \ {\var...
...\{ \displaystyle\frac { P \ cT \ - \ \vec{P} . \vec{R} }{\hbar} \right\} \ \ $}$](IMG418.GIF)