




Nächste Seite: Die Differentiale 2. Ordnung
Aufwärts: Die Differentiale erste und
Vorherige Seite: Die Differentiale 1. Ordnung
Inhalt
Index
Analog zu der Impulstheorie bildet der Vierergradient die Komponenten
der Tensorgradienten.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \displaystyle\frac {\partial}{\par...
...e\frac {\partial}{\partial y}, \displaystyle\frac {\partial}{\partial z})) \ $}$](IMG133.GIF) |
|
|
(2.61) |
Aus Bequemlichkeitsgründen führen wir für die partielle Ableitungen nach
den Koordinaten die Abkürzung
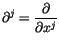 |
|
|
(2.62) |
ein. Analog lässt sich die Matrix des Vierergradiententensors der Energieheorie
darstellen:
Analog zur IT können wir für eine Lösung der partiellen
Differentialgleichung erster Ordnung
wie die linke Seite vom Viererimpuls schreiben :
Analog zu der IT können wir hier schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi\
= \ \psi_0 \ e^{{\displaystyl...
...ystyle ( \displaystyle\frac {P\, ct \ - \ \vec{p} . \vec{r}
}{\hbar} )}} \ \ $}$](IMG137.GIF) |
|
|
(2.63) |
Die Funktion 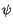 wird als die reelle Wellenfunktion bezeichnet.
Aus Analogie zu der Impulstheorie wird die Aussage unterstrichen, daß die Differential
eines Vierertensors ein Vierertensor ist. Die erste partielle Ableitungen eines
beliebigen Vierertensors
wird als die reelle Wellenfunktion bezeichnet.
Aus Analogie zu der Impulstheorie wird die Aussage unterstrichen, daß die Differential
eines Vierertensors ein Vierertensor ist. Die erste partielle Ableitungen eines
beliebigen Vierertensors 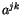 ist dann invariant, wenn sie mit dem
Vierertensor der Vierergeschwindigkeit der Energietheorie
multipliziert wird.
ist dann invariant, wenn sie mit dem
Vierertensor der Vierergeschwindigkeit der Energietheorie
multipliziert wird.
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\ d a^{jk} = ( \displaystyle\frac {\p...
...partial x^{jk}}a^{jk} ) \ d x^{jk} = ( \acute a^{jk} \ V^{jk} ) \ {ds}_j^k \ $}$](IMG140.GIF) |
|
|
(2.64) |





Nächste Seite: Die Differentiale 2. Ordnung
Aufwärts: Die Differentiale erste und
Vorherige Seite: Die Differentiale 1. Ordnung
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \displaystyle\frac {\partial}{\par...
...e\frac {\partial}{\partial y}, \displaystyle\frac {\partial}{\partial z})) \ $}$](IMG133.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \displaystyle\frac {\partial}{\par...
...e\frac {\partial}{\partial y}, \displaystyle\frac {\partial}{\partial z})) \ $}$](IMG133.GIF)
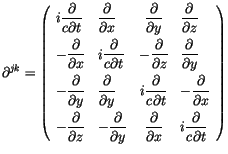
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi\
= \ \psi_0 \ e^{{\displaystyl...
...ystyle ( \displaystyle\frac {P\, ct \ - \ \vec{p} . \vec{r}
}{\hbar} )}} \ \ $}$](IMG137.GIF)
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\ d a^{jk} = ( \displaystyle\frac {\p...
...partial x^{jk}}a^{jk} ) \ d x^{jk} = ( \acute a^{jk} \ V^{jk} ) \ {ds}_j^k \ $}$](IMG140.GIF)