




Nächste Seite: Partielle Differentiale 1. Ordnung
Aufwärts: Die Differentiale erste und
Vorherige Seite: Partielle Differentiale 1. Ordnung
Inhalt
Index
Analog zu der Impulstheorie bildet der Quotient aus dem infinitesimalen
Viererortsvektor und dem skalaren Abstand der Vierergeschwindigkeit
, die wir an dieser Stelle als
das erste Differential des Viererortsvektors bezeichnen.
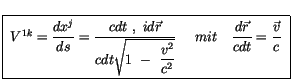 |
|
|
(2.52) |
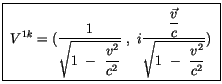 |
|
|
(2.53) |
Die Gleichung (2.53) ist die Komponente des Vierergeschwindigkeitstenors
der Energietheorie. Mit
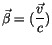 und analog zu der
Impulstheorie hat seine Matrix die Form:
und analog zu der
Impulstheorie hat seine Matrix die Form:
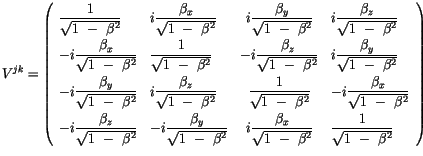 |
|
|
(2.54) |
Unter den Vierertensoren hat die Matrix der Vierergeschwindigkeitstensor 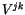 hat
einen besonderen Stellenwert. Ihr Quadrat bildet der Einheitstensor
hat
einen besonderen Stellenwert. Ihr Quadrat bildet der Einheitstensor
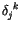 .
.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ V^{jk} \ . \ ( V^{jk} )^T = \ {\delta}_j^k \ $}$](IMG119.GIF) |
|
|
(2.55) |
Analog zu der Impulstheorie geben wir die Komponenten dieses Tensors an.
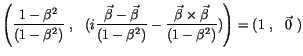 |
|
|
(2.56) |
Nun untersuchen wir in der Energietheorie das Distributivgesetz
der Vierertensoren. Das Produkt aus einem beliebigen Tensor
und dem Einheitstensor ist offenbar der Tensor selbst. Wir überprüfen diesen
Sachverhalt an Hand von zwei Transformationen.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ ( V^{jk} \ . \ V^{kj} ) \ . \ x^{kj} = V^{jk} \ . \ ( V^{kj} \ . \ x^{kj} ) \ $}$](IMG121.GIF) |
|
|
(2.57) |
Wie bereits gesehen ist der Klammerausdruck auf der linken Seite (2.57)
gleich dem Einheitstensor. Auf der rechten Seite finden wir zwei
Transformationen vor, die wir in zwei Schritten errechnen werden. Zur
besseren Übersicht würde die Subsitution
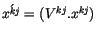 eingeführt. Wir errechnen die erste Transformation
und finden die Komponente des Klammerausdrucks:
eingeführt. Wir errechnen die erste Transformation
und finden die Komponente des Klammerausdrucks:
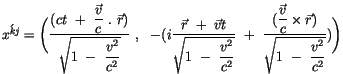 |
|
|
(2.58) |
Aus dem Produkt der Vierergschwindigkeit 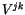 mit der transformierten
Viererortsmatrix
mit der transformierten
Viererortsmatrix
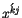 entsteht die zweite Transformation, die
den Viererortstensor in seiner Ausgangslage zurücktransformiert. Nach
der Ausführung der zweiten Transformation finden wir unter
Vernachlässigung einiger Glieder schießlich:
entsteht die zweite Transformation, die
den Viererortstensor in seiner Ausgangslage zurücktransformiert. Nach
der Ausführung der zweiten Transformation finden wir unter
Vernachlässigung einiger Glieder schießlich:
Der Vergleich mit der linken Seite in (2.57)
ergibt, daß in der ersten Klammer das Spatprodukt verschwindet und der Rest
gleich 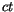 wird. in der zweiten Klammer ist der Ausdruck gleich -i
wird. in der zweiten Klammer ist der Ausdruck gleich -i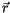 .
Der Vierervektor
.
Der Vierervektor 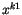 ist bei diesen Transformationen unverändert geblieben.
ist bei diesen Transformationen unverändert geblieben.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \vec{\beta} \ (\vec{\beta} \ . \ \...
... - \ \vec{\beta} \times ( \vec{\beta} \times \vec{r} ) = \beta^2 \ \vec{r} \ $}$](IMG131.GIF) |
|
|
(2.59) |
Die bei den äquivalenten Transformationen entstehenden Vektorkomponenten
haben die Form:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ {\bf grad } \ ( {\bf div} \ \vec{a} ) \ - \ {\bf rot} \ ( {\bf rot} \ \vec{a} ) = {\bf {grad}^2} \ \vec{a} \ $}$](IMG132.GIF) |
|
|
(2.60) |
Auch hier sind die anderen Darstellungen von (2.60) nicht zulässig, da
sonst die physikalische Inteperetationen zur Lichttheorie brüchig wird.





Nächste Seite: Partielle Differentiale 1. Ordnung
Aufwärts: Die Differentiale erste und
Vorherige Seite: Partielle Differentiale 1. Ordnung
Inhalt
Index
root
1999-07-07
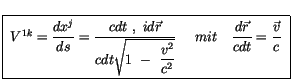
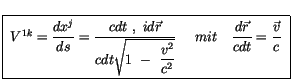

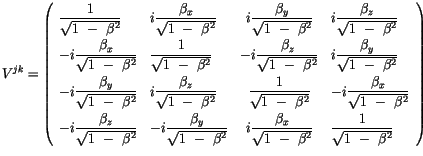
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ V^{jk} \ . \ ( V^{jk} )^T = \ {\delta}_j^k \ $}$](IMG119.GIF)
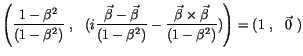
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ ( V^{jk} \ . \ V^{kj} ) \ . \ x^{kj} = V^{jk} \ . \ ( V^{kj} \ . \ x^{kj} ) \ $}$](IMG121.GIF)
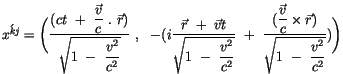
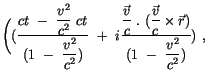
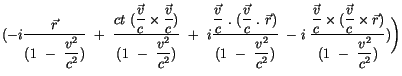
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ \vec{\beta} \ (\vec{\beta} \ . \ \...
... - \ \vec{\beta} \times ( \vec{\beta} \times \vec{r} ) = \beta^2 \ \vec{r} \ $}$](IMG131.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ {\bf grad } \ ( {\bf div} \ \vec{a} ) \ - \ {\bf rot} \ ( {\bf rot} \ \vec{a} ) = {\bf {grad}^2} \ \vec{a} \ $}$](IMG132.GIF)