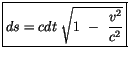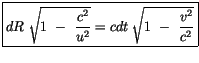Nächste Seite: Abstand in beliebigen Bezugssysteme
Aufwärts: Spiegelung der Vektoren
Vorherige Seite: Multiplikation der Vierertensoren
Inhalt
Index
Das Quadrat zweier infinitesimal benachbarter Viererortsvektoren wird in
der Impulstheorie als Quadrat ihres Abstands
bezeichnet.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ dS^2 = dR^2 \ - \ c^2 dT^2 \ $}$](IMG58.GIF) |
|
|
(2.26) |
Unter der Berücksichtigung den Ausdruck:
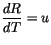 können wir für den Abstand schreiben:
können wir für den Abstand schreiben:
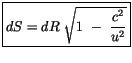 |
|
|
(2.27) |
Analog bezeichnen wir das Quadrat zweier infinitesimal benachbarter
Viererortsvektoren in der Energietheorie als Quadrat ihres Abstands.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}ds^2 = c^2 dt^2 \ - \ dr^2 $}$](IMG61.GIF) |
|
|
(2.28) |
An dieser Stelle klammern wir 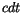 aus und unter Berücksichtigung der Beziehung
aus und unter Berücksichtigung der Beziehung
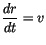 erhalten wir für den Abstand:
erhalten wir für den Abstand:
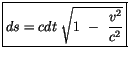 |
|
|
(2.29) |
Die Invarianz der Lichtgeschwindigkeit
bezüglich des dualen Abstands ist
eine der meistbestätigten Erfahrungen unserer Zeit durch das Expriment. Aus
diesem Sachverhalt folgt, daß der Abstand aus den dualen Bezugssystem gleich
sein muß. Folglich:
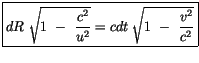 |
|
|
(2.30) |
Daraus schließen wir:
 |
|
|
(2.31) |
Der erste Therm in (2.31) stellt die Gleichheit der dualen Längen aus der
Impuls und Energietheorie dar.
Diese Erkenntnis hat die fundamentale Bedeutung für die Gleichheit des
Impulsbetrags zu dem Energie, die wir seiner Zeit besprechen werden.
In dem zweiten Term rechts erweist 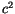 das doppellte Vorzeichen auf, von
dem wir das negative
vorerst verwerfen. Im Vakuum ist das Produkt
das doppellte Vorzeichen auf, von
dem wir das negative
vorerst verwerfen. Im Vakuum ist das Produkt 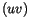 stets konstant.
In der dualen Physik (Impuls + Energietheorie) kann ein Teilchen jeder Geschwindigkeit aus dem Interval
stets konstant.
In der dualen Physik (Impuls + Energietheorie) kann ein Teilchen jeder Geschwindigkeit aus dem Interval
![$[0 \ , \ \infty]$](IMG69.GIF) annehmen. Es liegt nahe zu glauben, daß die Teilchengeschwindigkeit
unbegrenzt sei. Sie erstreckt sich zwar von Null bis zum unendlichen, die aber
an der Stelle
annehmen. Es liegt nahe zu glauben, daß die Teilchengeschwindigkeit
unbegrenzt sei. Sie erstreckt sich zwar von Null bis zum unendlichen, die aber
an der Stelle 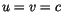 einen Sprung aufweist. solche Schlußfolgerungen
erweisen sich als falsch.
Richtig ist die Aussage daß die Geschwindigkeit
einen Sprung aufweist. solche Schlußfolgerungen
erweisen sich als falsch.
Richtig ist die Aussage daß die Geschwindigkeit 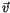 eines Teilchens
oder auch Gruppengeschwindigkeit
genannt alle Werte unterhalb der
c-Barriere aus dem Interval
eines Teilchens
oder auch Gruppengeschwindigkeit
genannt alle Werte unterhalb der
c-Barriere aus dem Interval ![$[0 \ , \ c]$](IMG71.GIF) annimmt dagegen aber
die Geschwindigkeit
annimmt dagegen aber
die Geschwindigkeit 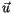 die Phasengeschwindigkeit
genannt alle
Werte über die Lichgeschwindigkeitgerenze aus dem Interval
die Phasengeschwindigkeit
genannt alle
Werte über die Lichgeschwindigkeitgerenze aus dem Interval
![$[c \ , \ \infty]$](IMG73.GIF) annehmen
kann.
Die Gruppengeschwindigkeit und die Phasengeschwindigkeit werden
als duale Geschwindigkeit der Materie oder Antimaterie bezeichnet,
die uns häufiger beschäftigen werden.
annehmen
kann.
Die Gruppengeschwindigkeit und die Phasengeschwindigkeit werden
als duale Geschwindigkeit der Materie oder Antimaterie bezeichnet,
die uns häufiger beschäftigen werden.





Nächste Seite: Abstand in beliebigen Bezugssysteme
Aufwärts: Spiegelung der Vektoren
Vorherige Seite: Multiplikation der Vierertensoren
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ dS^2 = dR^2 \ - \ c^2 dT^2 \ $}$](IMG58.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ dS^2 = dR^2 \ - \ c^2 dT^2 \ $}$](IMG58.GIF)
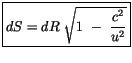
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}ds^2 = c^2 dt^2 \ - \ dr^2 $}$](IMG61.GIF)