Nächste Seite: Die Differentiale erste und
Aufwärts: Spiegelung der Vektoren
Vorherige Seite: Der Abstand
Inhalt
Index
Die Vierervektoren der beliebigen Bezugssysteme für die Materie (Antimaterie)
haben einen Komplexen Charakter. Gemäß (1.7) können wir schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ_j^k \ = \ (d X_j) \ + \ (dx^k) \ \ $}\quad \mbox{f\uml {u}r} \ j=k$](IMG74.GIF) |
|
|
(2.32) |
Im vorab kann man sagen, daß der Mittelwert aus dem Quadrat dieses komplexen
Viererortsvektors dem Abstandquadrat  gleichkommen muß. Für das Quadrat
des infinitesimalen Achterortsvektors (2.32) finden wir :
gleichkommen muß. Für das Quadrat
des infinitesimalen Achterortsvektors (2.32) finden wir :
 |
|
|
(2.33) |
Unter der Berücksichtigung von (2.31) gilt :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(c^2 dt dT \ - \ d\vec{R} . d\vec{r}) \ = \ 0 \ \ \ \ $}$](IMG78.GIF) |
|
|
(2.34) |
Die erhaltenen Restglieder lauten :
 |
|
|
(2.35) |
Analog kann man für die Antimaterie gemäß (1.9) schreiben:
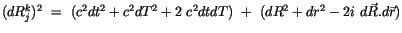 |
|
|
(2.36) |
Unter der Berücksichtigung (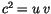 ) gilt:
) gilt:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(c^2 dt dT \ - \ d\vec{R} . d\vec{r}) \ = \ 0 \ \ \ \ $}$](IMG78.GIF) |
|
|
(2.37) |
Die erhaltenen Restglieder lauten auch hier:
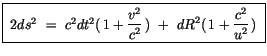 |
|
|
(2.38) |





Nächste Seite: Die Differentiale erste und
Aufwärts: Spiegelung der Vektoren
Vorherige Seite: Der Abstand
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ_j^k \ = \ (d X_j) \ + \ (dx^k) \ \ $}\quad \mbox{f\uml {u}r} \ j=k$](IMG74.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dZ_j^k \ = \ (d X_j) \ + \ (dx^k) \ \ $}\quad \mbox{f\uml {u}r} \ j=k$](IMG74.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(c^2 dt dT \ - \ d\vec{R} . d\vec{r}) \ = \ 0 \ \ \ \ $}$](IMG78.GIF)
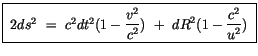
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(c^2 dt dT \ - \ d\vec{R} . d\vec{r}) \ = \ 0 \ \ \ \ $}$](IMG78.GIF)