




Nächste Seite: Die makroskopische Physik
Aufwärts: Das Atom in der
Vorherige Seite: Der Viererimpuls des gebundenen
Inhalt
Index
Die radiale Wellenfunktion
Die endgültige Form der radialen Differentialgleichung des gebundenen
Teilchens mit dem Beitrag der Winkelfunktionen (10.65) lautet:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \hbar^2(\displaystyle\frac ...
... l + s )^2 (\displaystyle\frac {\hbar}{r})^2\, \right) R_r = 2 p^2_{(r)} R_r $}$](IMG868.GIF) |
|
|
(13.12) |
mit Hilfe von
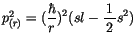 (10.45)und
(10.45)und
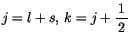 kann man diese Gleichung in seiner endgültigen Form
schreiben:
kann man diese Gleichung in seiner endgültigen Form
schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \hbar^2(\displaystyle\frac ...
...0 - (\, k^2-1\,) (\displaystyle\frac {\hbar}{r})^2\, \right)\, R_r \, = \, 0 $}$](IMG871.GIF) |
|
|
(13.13) |
Wir werden diese Gleichung gemäss (4.43) linalisieren und führen zuerst
genräll für das Term die potentielle Energie die Buchstabe V ein und spalten
weiterhin die radialle Wellenfunktion in
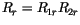 auf.
auf.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \displaystyle\frac {d^2}{dr^2}+\...
...aystyle\frac {\, E\, }{c}- \displaystyle\frac {V}{c})^2 \, ) R_{1r}R_{2r} \, $}$](IMG873.GIF) |
|
|
(13.14) |
Hieraus ergeben sich zwei linerare Differentialgleichungen unseres Eigenwertproblems:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \displaystyle\frac {\, d\, }{d r...
...}{r}\, ) R_{1r} \, = \, \displaystyle\frac {1}{\hbar c}(\, E-V+E_0\, )R_{2r} $}$](IMG874.GIF) |
|
|
(13.15) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \displaystyle\frac {\, d\, }{d r...
...r}\, ) R_{2r} \, = \, \displaystyle\frac {1}{\hbar c} (\, -E+V+E_0\, )R_{1r} $}$](IMG875.GIF) |
|
|
(13.16) |
Für die kleine Geschwindigkeiten 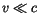 kann man aus (13.15) mit
kann man aus (13.15) mit
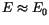 ,
, 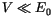 die Übergang zu der sogennaten
nichtrelativistischen
Schrödinger Gleichung herleiten:
die Übergang zu der sogennaten
nichtrelativistischen
Schrödinger Gleichung herleiten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{2r} = \displaystyle\frac {\hbar}{...
...laystyle\frac {\, d\, }{d r}+ \displaystyle\frac {1+k}{r}\, )\, R_{1r} \quad $}$](IMG879.GIF) |
|
|
(13.17) |
und beim einsetzen diese Gleichung in (13.16) und mit 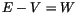 bzw.
bzw. 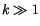 findet man schließlich:
findet man schließlich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {d^2}{dr^2}+\dis...
...m_0}{\hbar^2}(W-V)\, - \, \displaystyle\frac {k(k-1)}{r^2})\, R_{1r} = \ 0 \ $}$](IMG882.GIF) |
|
|
(13.18) |
wobei k mit l zu identifizieren ist. Für 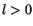 gilt:
gilt:
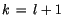 |
|
|
(13.19) |
Wir interessieren uns aber zuerst für die asymptotischen Lösungen der linearisierten
Differentialgleichungen (13.15) und (13.16) in Form
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{1r} \, = \, {V_0}_1 \ e^{-\displa...
...2r} \, = \, {V_0}_2 \ e^{-\displaystyle (\displaystyle\frac {r}{r_0})} \quad $}$](IMG885.GIF) |
|
|
(13.20) |
Für die Bestimmung der Größen 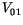 ,
, 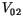 und in Exponenten
stehende Größe
und in Exponenten
stehende Größe 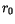 streichen wir in (13.15) und (13.16) alle Glieder
mit
streichen wir in (13.15) und (13.16) alle Glieder
mit
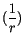 sowie
sowie 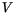 und erhalten:
und erhalten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\, d\, }{d r}R_{1r} \, = \, \displaystyle\frac {1}{\hbar c}(\, E + E_0\, )R_{2r} $}$](IMG890.GIF) |
|
|
(13.21) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\, d\, }{d r}R_{2r} \, = \, \displaystyle\frac {1}{\hbar c} (\, -E + E_0\, )R_{1r} $}$](IMG891.GIF) |
|
|
(13.22) |
Nach Einsetzen der asymptotischen Lösungen in den beiden letzten Gleichungen
finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-(\displaystyle\frac {1}{r_0})\, {V_0}_1 \, = \, \displaystyle\frac {1}{\hbar c} (\, E + E_0 \, ) \, {V_0}_2 \ $}$](IMG892.GIF) |
|
|
(13.23) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-(\displaystyle\frac {1}{r_0})\, {V_0}_2 \, = \, \displaystyle\frac {1}{\hbar c} (\, -E + E_0 \, ) \, {V_0}_1 \ $}$](IMG893.GIF) |
|
|
(13.24) |
folglich finden wir für den Exponenten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {1}{r_0}) \, = \, +\displaystyle\frac {\, \sqrt{\, E^2_0 \, - \, E^2\, }}{\hbar c} \quad $}$](IMG894.GIF) |
|
|
(13.25) |
Nun benutzen wir als unabhängige Variable
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho \, = \, (\displaystyle\frac {r}{r_0}) \qquad $}$](IMG895.GIF) |
|
|
(13.26) |
und rechnen an Stelle den asymptotischen, mit der exakten Lösungen
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_1 \, = \, V_1 \, e^{-\varrho} \quad \quad $}$](IMG896.GIF) |
|
|
(13.27) |
so wie
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_2 \, = \, V_2 \, e^{-\varrho} \quad $}$](IMG897.GIF) |
|
|
(13.28) |
weiter. Vorerst bezeichnen wir mit 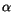 , die Feinstrukturkonstante
( A. Sommerfeld):
, die Feinstrukturkonstante
( A. Sommerfeld):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\alpha = \ \displaystyle\frac {e^2\,}{2\, \varepsilon_0 \, c\, h}\quad $}$](IMG898.GIF) |
|
|
(13.29) |
Folglich erhalten wir unter dieser Einführung für die Gleichungen (13.15) und
(13.16)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V_1'+ (\, \displaystyle\frac {1-k}{\...
...pha Z}{\varrho} + \displaystyle\frac {E_0 + E}{\sqrt{E^2_0 - E^2}} \, )V_2 \ $}$](IMG899.GIF) |
|
|
(13.30) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V_2'+ (\, \displaystyle\frac {1+k}{\...
...pha Z}{\varrho} + \displaystyle\frac {E_0 - E}{\sqrt{E^2_0 - E^2}} \, )V_1 \ $}$](IMG900.GIF) |
|
|
(13.31) |
Für 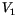 und
und 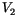 machen wir folgenden Ansatz
machen wir folgenden Ansatz
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V_1 \, = \, \varrho^\gamma \sum\limi...
...\, = \, \varrho^\gamma \sum\limits_{\nu=0}^\infty b_\nu \, \varrho^\nu \quad $}$](IMG903.GIF) |
|
|
(13.32) |
Um die charakteristische Gleichung für den Exponenten im Nullpunkt zu finden,
tragen wir 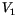 und
und 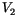 in (13.30) und (13.31) ein und vergleichen den
Koeffizienten von
in (13.30) und (13.31) ein und vergleichen den
Koeffizienten von
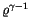 auf beiden Seiten:
auf beiden Seiten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\gamma +1 -k)a_0 = \alpha Z b_0\, , \ \, (\gamma +1 +k)b_0 = -\alpha Z a_0 \ $}$](IMG905.GIF) |
|
|
(13.33) |
Nun leiten wir die Relinearisierung ein und multiplizieren die beide Gleichungen,
so finden wir die quadratische Form:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \gamma + 1\, )^2 \, - \, k^2 \, = \, -\alpha^2 Z^2 \ $}$](IMG906.GIF) |
|
|
(13.34) |
und schließlich erhalten wir für die Wahl des positiven Vorzeichens:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\gamma + 1 \, = \, + \, \sqrt{\, k^2 \, - \, \alpha^2 Z^2 \, } \quad $}$](IMG907.GIF) |
|
|
(13.35) |
Nun werden wir für 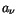 ,
, 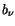 die zugehörige Rekursionformel ermitteln.
Dazu werden wir die Koeffizienten der Potenz
die zugehörige Rekursionformel ermitteln.
Dazu werden wir die Koeffizienten der Potenz
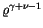 in den
Gleichungen (13.30) und (13.31) in beiden Seiten einander gleichsetzen.
Führen wir für
in den
Gleichungen (13.30) und (13.31) in beiden Seiten einander gleichsetzen.
Führen wir für
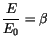 ein, so gilt offenbar die Beziehung:
ein, so gilt offenbar die Beziehung:
 |
|
|
(13.36) |
Nun ordnen wir die 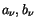 in wachsender Richtung von
in wachsender Richtung von 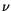 ein
ein
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}a_{\nu-1} \, + \, w\, b_{\nu-1} \, = \, (\gamma + \nu + 1 - k)a_\nu \, - \, \alpha Z \, b_\nu \quad $}$](IMG914.GIF) |
|
|
(13.37) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}w^{-1}\, a_{\nu-1} \, + \, b_{\nu-1} \, = \, (\gamma + \nu + 1 + k )b_\nu \, + \, \alpha Z \, a_\nu \quad $}$](IMG915.GIF) |
|
|
(13.38) |
Multiplizieren wir die zweite Gleichung (13.38) mit 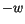 und addieren sie zu der
ersten (13.38), so finden wir:
und addieren sie zu der
ersten (13.38), so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {a_\nu}{b_\nu} \,...
...\gamma + \nu + 1 + k\, )}{(\, \gamma + \nu + 1 - k\, ) - w\, \alpha Z} \quad $}$](IMG917.GIF) |
|
|
(13.39) |
Diese ist eine Verhältnisgleichung mit zwei Unbekannten 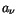 und
und 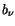 ,
die wir so nicht ohne weiters lösen können. Die zweite Verhältnisgleichung
hierzu gewinnen wir, in dem wir die linken Seiten von (13.37) und (13.38)
einzeln zu verschwinden brinngen und
,
die wir so nicht ohne weiters lösen können. Die zweite Verhältnisgleichung
hierzu gewinnen wir, in dem wir die linken Seiten von (13.37) und (13.38)
einzeln zu verschwinden brinngen und 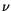 durch
durch 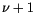 ersetzen.
ersetzen.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {a_{\nu-1}}{b_{\n...
...u + 1}) \quad (\displaystyle\frac {a_{\nu}}{b_{\nu}}) \, = \, -w \quad \quad $}$](IMG919.GIF) |
|
|
(13.40) |
Diese beiden letzten Beziehungen (13.39) und (13.40) erfüllen die Bedingung zum
abberechen der Potenzreihen (13.32) bei dem 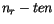 Glied. Hieraus folgt:
Glied. Hieraus folgt:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\gamma + 1 + n_r + k + (\displaystyle\frac {\alpha Z}{w}) + \gamma + 1 + n_r - k - w\, \alpha Z \, = \, 0 \quad $}$](IMG921.GIF) |
|
|
(13.41) |
Führen wir für 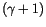 die äquivalente Beziehung (13.35) ein und
ziehen die
die äquivalente Beziehung (13.35) ein und
ziehen die 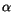 - Werte zusammen, so finden wir:
- Werte zusammen, so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}n_r + \sqrt{k^2 - \alpha^2 Z^2} \, =...
...laystyle\frac {1}{\, 2 \, }\alpha Z (\, w - \displaystyle\frac {1}{w}) \quad $}$](IMG923.GIF) |
|
|
(13.42) |
Für die runde Klammer in der rechten Seite erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {1+\beta}{\sqrt{1...
...sqrt{1-\beta^2}} \, = \, 2 \, \displaystyle\frac {1}{\sqrt{\beta^2-1}} \quad $}$](IMG924.GIF) |
|
|
(13.43) |
Quadrieren wir nun (13.42) und stellen wir die Gleichung nach
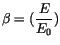 um, so ergibt sich:
um, so ergibt sich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {E}{E_0})^2 \, =...
...ha^2 Z^2}{(n_r + \sqrt{\, k^2 \, - \, \alpha^2 Z^2\, })^2}\right)^{-1} \quad $}$](IMG926.GIF) |
|
|
(13.44) |
Nun werden wir die radiale Quantenzahl 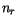 in Hauptquantenzahl
in Hauptquantenzahl 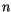 umschreiben.
umschreiben.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}n \, = \, n_r + (\, j+\displaystyle\...
... l+s \quad \mbox{und} \quad k\, = \, j+\displaystyle\frac {1}{\, 2 \, }\quad $}$](IMG929.GIF) |
|
|
(13.45) |
Nach Wurzelziehen auf beiden Seiten in (13.44) erhalten wir für die Atomhülle
die sogenannte Feinstruktur Formel:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}E_{nj} \, = \, E_0 \, \left( \, 1 \,...
... {1}{\, 2 \, })^2 \, - \, \alpha^2 Z^2}\, \right)^2}\right)^{-\frac{1}{2}} \ $}$](IMG930.GIF) |
|
|
(13.46) |
Dabei nehmen die zwei Quantenzahlen folgende Werte an.
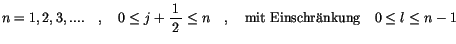 |
|
|
(13.47) |
Entwickeln wir (13.46) nach Potenzen von 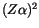 , so finden wir:
, so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}E_{nj} \, = \, E_0 \left\{ 1-\displa...
...isplaystyle\frac {3}{4n}\right)\right] + 0 \, ((Z\alpha)^6) \, \right\}\quad $}$](IMG933.GIF) |
|
|
(13.48) |
Die Beziehung (13.46) war bei den Beobachtungen am H-Atom bis zur Mitte unseres
Jahrhunderts zufriedenstellend.
Lamb und Retherford bestätigten 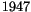 mit den Messungen der Feinstruktur
des H-Atoms eine Verschiebung des
mit den Messungen der Feinstruktur
des H-Atoms eine Verschiebung des 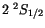 Niveaus nach oben gegenüber den
Niveaus nach oben gegenüber den
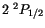 Linien.
Offenbar fällt in (13.48) der Feinstruktur-Term
(die rechteckige Klammer) größer aus als im Experiment der Fall ist.
Diese Größenordnung liegt bei etwa
Linien.
Offenbar fällt in (13.48) der Feinstruktur-Term
(die rechteckige Klammer) größer aus als im Experiment der Fall ist.
Diese Größenordnung liegt bei etwa
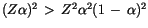 Der zweite Term ist aus der resultierenden potentiellen Energie
Der zweite Term ist aus der resultierenden potentiellen Energie
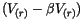 in (7.29) entstanden. Wir ergänzen den
in (7.29) entstanden. Wir ergänzen den
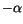 -Wert in diesem Term mit dem Elektronenspin
-Wert in diesem Term mit dem Elektronenspin 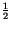 , den wir
mit der Hilfsgröße
, den wir
mit der Hilfsgröße 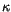 bezeichnen.
Unter Vernachlässigung der runden Klammer in (13.48) sagt die Theorie eine
Abhängigkeit der Lamb-Shift
bezeichnen.
Unter Vernachlässigung der runden Klammer in (13.48) sagt die Theorie eine
Abhängigkeit der Lamb-Shift
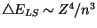 voraus, die auch
für die normale Feinstruktur-Aufspaltung gültig ist. Die resultierende
Energieverschiebung ist demnach:
voraus, die auch
für die normale Feinstruktur-Aufspaltung gültig ist. Die resultierende
Energieverschiebung ist demnach:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\triangle E_{LS} \, = \, \left(2\, \...
... \alpha^2}{n^3}\right) \ \displaystyle\frac {1}{\, 2 \, }\, E_0 \ \alpha^2 \ $}$](IMG943.GIF) |
|
|
(13.49) |
Die typischen Werte sind
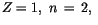 und
und 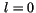 . Diese positive
Energie erklärt die Verschiebung der
. Diese positive
Energie erklärt die Verschiebung der 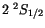 Linien
des Wasserstoffatoms nach oben gegenüber des
Linien
des Wasserstoffatoms nach oben gegenüber des 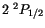 Niveaus.
Niveaus.





Nächste Seite: Die makroskopische Physik
Aufwärts: Das Atom in der
Vorherige Seite: Der Viererimpuls des gebundenen
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \hbar^2(\displaystyle\frac ...
... l + s )^2 (\displaystyle\frac {\hbar}{r})^2\, \right) R_r = 2 p^2_{(r)} R_r $}$](IMG868.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \hbar^2(\displaystyle\frac ...
... l + s )^2 (\displaystyle\frac {\hbar}{r})^2\, \right) R_r = 2 p^2_{(r)} R_r $}$](IMG868.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, \hbar^2(\displaystyle\frac ...
...0 - (\, k^2-1\,) (\displaystyle\frac {\hbar}{r})^2\, \right)\, R_r \, = \, 0 $}$](IMG871.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \displaystyle\frac {d^2}{dr^2}+\...
...aystyle\frac {\, E\, }{c}- \displaystyle\frac {V}{c})^2 \, ) R_{1r}R_{2r} \, $}$](IMG873.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \displaystyle\frac {\, d\, }{d r...
...}{r}\, ) R_{1r} \, = \, \displaystyle\frac {1}{\hbar c}(\, E-V+E_0\, )R_{2r} $}$](IMG874.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \displaystyle\frac {\, d\, }{d r...
...r}\, ) R_{2r} \, = \, \displaystyle\frac {1}{\hbar c} (\, -E+V+E_0\, )R_{1r} $}$](IMG875.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{2r} = \displaystyle\frac {\hbar}{...
...laystyle\frac {\, d\, }{d r}+ \displaystyle\frac {1+k}{r}\, )\, R_{1r} \quad $}$](IMG879.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {d^2}{dr^2}+\dis...
...m_0}{\hbar^2}(W-V)\, - \, \displaystyle\frac {k(k-1)}{r^2})\, R_{1r} = \ 0 \ $}$](IMG882.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{1r} \, = \, {V_0}_1 \ e^{-\displa...
...2r} \, = \, {V_0}_2 \ e^{-\displaystyle (\displaystyle\frac {r}{r_0})} \quad $}$](IMG885.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\, d\, }{d r}R_{1r} \, = \, \displaystyle\frac {1}{\hbar c}(\, E + E_0\, )R_{2r} $}$](IMG890.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\, d\, }{d r}R_{2r} \, = \, \displaystyle\frac {1}{\hbar c} (\, -E + E_0\, )R_{1r} $}$](IMG891.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-(\displaystyle\frac {1}{r_0})\, {V_0}_1 \, = \, \displaystyle\frac {1}{\hbar c} (\, E + E_0 \, ) \, {V_0}_2 \ $}$](IMG892.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-(\displaystyle\frac {1}{r_0})\, {V_0}_2 \, = \, \displaystyle\frac {1}{\hbar c} (\, -E + E_0 \, ) \, {V_0}_1 \ $}$](IMG893.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {1}{r_0}) \, = \, +\displaystyle\frac {\, \sqrt{\, E^2_0 \, - \, E^2\, }}{\hbar c} \quad $}$](IMG894.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\varrho \, = \, (\displaystyle\frac {r}{r_0}) \qquad $}$](IMG895.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_1 \, = \, V_1 \, e^{-\varrho} \quad \quad $}$](IMG896.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_2 \, = \, V_2 \, e^{-\varrho} \quad $}$](IMG897.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\alpha = \ \displaystyle\frac {e^2\,}{2\, \varepsilon_0 \, c\, h}\quad $}$](IMG898.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V_1'+ (\, \displaystyle\frac {1-k}{\...
...pha Z}{\varrho} + \displaystyle\frac {E_0 + E}{\sqrt{E^2_0 - E^2}} \, )V_2 \ $}$](IMG899.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V_2'+ (\, \displaystyle\frac {1+k}{\...
...pha Z}{\varrho} + \displaystyle\frac {E_0 - E}{\sqrt{E^2_0 - E^2}} \, )V_1 \ $}$](IMG900.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}V_1 \, = \, \varrho^\gamma \sum\limi...
...\, = \, \varrho^\gamma \sum\limits_{\nu=0}^\infty b_\nu \, \varrho^\nu \quad $}$](IMG903.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\gamma +1 -k)a_0 = \alpha Z b_0\, , \ \, (\gamma +1 +k)b_0 = -\alpha Z a_0 \ $}$](IMG905.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\, \gamma + 1\, )^2 \, - \, k^2 \, = \, -\alpha^2 Z^2 \ $}$](IMG906.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\gamma + 1 \, = \, + \, \sqrt{\, k^2 \, - \, \alpha^2 Z^2 \, } \quad $}$](IMG907.GIF)

![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}a_{\nu-1} \, + \, w\, b_{\nu-1} \, = \, (\gamma + \nu + 1 - k)a_\nu \, - \, \alpha Z \, b_\nu \quad $}$](IMG914.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}w^{-1}\, a_{\nu-1} \, + \, b_{\nu-1} \, = \, (\gamma + \nu + 1 + k )b_\nu \, + \, \alpha Z \, a_\nu \quad $}$](IMG915.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {a_\nu}{b_\nu} \,...
...\gamma + \nu + 1 + k\, )}{(\, \gamma + \nu + 1 - k\, ) - w\, \alpha Z} \quad $}$](IMG917.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {a_{\nu-1}}{b_{\n...
...u + 1}) \quad (\displaystyle\frac {a_{\nu}}{b_{\nu}}) \, = \, -w \quad \quad $}$](IMG919.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\gamma + 1 + n_r + k + (\displaystyle\frac {\alpha Z}{w}) + \gamma + 1 + n_r - k - w\, \alpha Z \, = \, 0 \quad $}$](IMG921.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}n_r + \sqrt{k^2 - \alpha^2 Z^2} \, =...
...laystyle\frac {1}{\, 2 \, }\alpha Z (\, w - \displaystyle\frac {1}{w}) \quad $}$](IMG923.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {1+\beta}{\sqrt{1...
...sqrt{1-\beta^2}} \, = \, 2 \, \displaystyle\frac {1}{\sqrt{\beta^2-1}} \quad $}$](IMG924.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(\displaystyle\frac {E}{E_0})^2 \, =...
...ha^2 Z^2}{(n_r + \sqrt{\, k^2 \, - \, \alpha^2 Z^2\, })^2}\right)^{-1} \quad $}$](IMG926.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}n \, = \, n_r + (\, j+\displaystyle\...
... l+s \quad \mbox{und} \quad k\, = \, j+\displaystyle\frac {1}{\, 2 \, }\quad $}$](IMG929.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}E_{nj} \, = \, E_0 \, \left( \, 1 \,...
... {1}{\, 2 \, })^2 \, - \, \alpha^2 Z^2}\, \right)^2}\right)^{-\frac{1}{2}} \ $}$](IMG930.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}E_{nj} \, = \, E_0 \left\{ 1-\displa...
...isplaystyle\frac {3}{4n}\right)\right] + 0 \, ((Z\alpha)^6) \, \right\}\quad $}$](IMG933.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\triangle E_{LS} \, = \, \left(2\, \...
... \alpha^2}{n^3}\right) \ \displaystyle\frac {1}{\, 2 \, }\, E_0 \ \alpha^2 \ $}$](IMG943.GIF)