




Nächste Seite: Die radiale Wellenfunktion
Aufwärts: Das Atom in der
Vorherige Seite: Das Atom in der
Inhalt
Index
Der Viererimpuls des gebundenen Teilchens der ET läßt sich aus der
Addition des mechanischen und elektromagnetischen Viererimpulses der ET gewinnen.
Unter der Berücksichtigung von
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi = \ \psi_0 \ {\bf exp} \left\{ ...
...tyle\frac {\, \varepsilon\, }{c})\, ct + \vec{r} . \vec{p} }{\hbar} \right\} $}$](IMG853.GIF) |
|
|
(13.1) |
und
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}e_m = e^- \ R_V \quad , \quad \vec{p...
...aystyle\frac {V^-_{(r)}}{c} \quad , \quad \psi\, . \, (\psi^*) = \, \psi^2_0 $}$](IMG854.GIF) |
|
|
(13.2) |
erhält man die Differentialgleichung des gebundenen Teilchens:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (-\hbar\displaystyle\frac ...
... (\psi)^* \psi \ = \ \left( \, P \ , \ i\vec{p} \, \right) (\psi^*) \psi \ $}\ $](IMG855.GIF) |
|
|
(13.3) |
Nach eliminieren der zeitlichen Gradienten mit 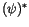 erhalten wir:
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (\displaystyle\frac {\, E\...
... grad} - \vec{p}_m) \, \right) \ = \ \left( \, P \ , \ i\vec{p} \, \right) \ $}$](IMG857.GIF) |
|
|
(13.4) |
Offenbar ist das zweifache Tensorprodukt
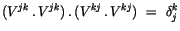 |
|
|
(13.5) |
gleich dem Einheitstensor. Die Klammerausdrücke bilden neue Vierertensoren, die
bei der Problemstellung diskreter Zustände ihre Anwendung finden. Bilden wir
das äquivalente Tensorprodukt mit der Beziehung (13.4), so finden wir für seine
linke Seite:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (\displaystyle\frac {\, E\...
... \displaystyle\frac {V^-_{(r)}}{c}) (\hbar{\sf grad} - \vec{p}_m)\,\right) \ $}$](IMG859.GIF) |
|
|
(13.6) |
äquivalente Komponente finden wir für die rechte Seite von (13.4):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( (\, p^2 \ + \ P^2 \, ) \ , \ \ (\, i2\, P\, \vec{p}\, )\right) \quad $}$](IMG860.GIF) |
|
|
(13.7) |
Aus dem Vergleich der Gleichungen in (13.6) und (13.7) schließen wir auf die
skalare
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (\displaystyle\frac {\, E\...
... \ (\hbar{\sf grad} - \vec{p}_m)^2\right) \ = \ (\, p^2 \ + \ P^2 \, ) \quad $}$](IMG861.GIF) |
|
|
(13.8) |
und Vektorkomponenten
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, i2\, P\, \vec{p}\, \right)...
...displaystyle\frac {V^-_{(r)}}{c}) (\hbar{\bf grad} - \vec{p}_m)\right) \quad $}$](IMG862.GIF) |
|
|
(13.9) |
Wir interessieren uns für die skalare Komponetene dieses Tensorprodukts.
Addieren wir auf beide Seiten von (13.8) 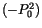 hinzu, so können wir
mit
hinzu, so können wir
mit 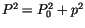 die rechte Seite in
die rechte Seite in 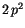 umschreiben. Anschließend
multiplizieren wir beiden Seiten der Gleichung mit
umschreiben. Anschließend
multiplizieren wir beiden Seiten der Gleichung mit 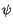 , so erhalten wir die
Wellengleichung:
, so erhalten wir die
Wellengleichung:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, (\hbar{\sf grad} - \vec{p}_...
...le\frac {V^-_{(r)}}{c})^2 \ - \ P^2_0 \, \right)\, \psi \ = \ 2\, p^2\, \psi $}$](IMG865.GIF) |
|
|
(13.10) |
Für den stationären Zustand der Wellengleichung, also das Verschwinden aller
zeitabhängigen Glieder 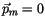 erhalten wir:
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, (\hbar{\sf grad} )^2 \ + \ ...
...2 \ - \ P^2_0 \, \right)\, \psi \ = \ 2\, p^2_{(r,\vartheta,\varphi)}\, \psi $}$](IMG867.GIF) |
|
|
(13.11) |





Nächste Seite: Die radiale Wellenfunktion
Aufwärts: Das Atom in der
Vorherige Seite: Das Atom in der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi = \ \psi_0 \ {\bf exp} \left\{ ...
...tyle\frac {\, \varepsilon\, }{c})\, ct + \vec{r} . \vec{p} }{\hbar} \right\} $}$](IMG853.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\psi = \ \psi_0 \ {\bf exp} \left\{ ...
...tyle\frac {\, \varepsilon\, }{c})\, ct + \vec{r} . \vec{p} }{\hbar} \right\} $}$](IMG853.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}e_m = e^- \ R_V \quad , \quad \vec{p...
...aystyle\frac {V^-_{(r)}}{c} \quad , \quad \psi\, . \, (\psi^*) = \, \psi^2_0 $}$](IMG854.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (-\hbar\displaystyle\frac ...
... (\psi)^* \psi \ = \ \left( \, P \ , \ i\vec{p} \, \right) (\psi^*) \psi \ $}\ $](IMG855.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (\displaystyle\frac {\, E\...
... grad} - \vec{p}_m) \, \right) \ = \ \left( \, P \ , \ i\vec{p} \, \right) \ $}$](IMG857.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (\displaystyle\frac {\, E\...
... \displaystyle\frac {V^-_{(r)}}{c}) (\hbar{\sf grad} - \vec{p}_m)\,\right) \ $}$](IMG859.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( (\, p^2 \ + \ P^2 \, ) \ , \ \ (\, i2\, P\, \vec{p}\, )\right) \quad $}$](IMG860.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, (\displaystyle\frac {\, E\...
... \ (\hbar{\sf grad} - \vec{p}_m)^2\right) \ = \ (\, p^2 \ + \ P^2 \, ) \quad $}$](IMG861.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left( \, i2\, P\, \vec{p}\, \right)...
...displaystyle\frac {V^-_{(r)}}{c}) (\hbar{\bf grad} - \vec{p}_m)\right) \quad $}$](IMG862.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, (\hbar{\sf grad} - \vec{p}_...
...le\frac {V^-_{(r)}}{c})^2 \ - \ P^2_0 \, \right)\, \psi \ = \ 2\, p^2\, \psi $}$](IMG865.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\left(\, (\hbar{\sf grad} )^2 \ + \ ...
...2 \ - \ P^2_0 \, \right)\, \psi \ = \ 2\, p^2_{(r,\vartheta,\varphi)}\, \psi $}$](IMG867.GIF)