



Nächste Seite: Spiegelung der Vektoren
Aufwärts: Die Tensoren
Vorherige Seite: Die Tensoren
Inhalt
Index
Im dreidimensionalen kartesischen Raum
ist der
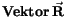 durch seine
drei skalaren Komponenten
durch seine
drei skalaren Komponenten
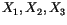 und
und
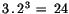 Einheitsvektoren = zweimal 12 Richtungen2.1
Einheitsvektoren = zweimal 12 Richtungen2.1
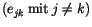 im Raum von Betrag 1 völlig bestimmt (
im Raum von Betrag 1 völlig bestimmt ( Richtungen fallen mit der
Richtungen der entsprechenden Achsen überein). Der Vektor
Richtungen fallen mit der
Richtungen der entsprechenden Achsen überein). Der Vektor
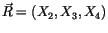 |
|
|
(2.1) |
hat positive Komponenten mit 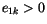 . Für
. Für 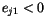 erhalten wir :
erhalten wir :
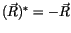 |
|
|
(2.2) |
Sein Quadrat erhalten wir aus dem eigenen skalaren Produkt.
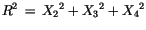 |
|
|
(2.3) |
Der Betrag eines beliebigen Ortsvektor lautet:
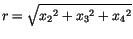 |
|
|
(2.4) |
Das Produkt eines Vektors mit einem Skalar ( die Paralellverschiebung)
und das Vektorprodukt
sind zwei weitere Vektorverknüpfungen, die
aber zur Änderung seiner Lage im Raum führen. Bei einem Eigenprodukt
entstehende polarer
und axialer
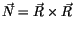 |
|
|
(2.6) |
Vektor bezeichen wir als Nullvektor
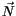 da bekanntlich
seine Lage dadurch unverändert bleibt.
Fasst man die Formel (2.1) und (2.4) in einem Schema oder einer
Matrix zusammen, so besitzt diese eine affine Transformationseigenschaft,
die bei einer Anwendung auf sich selbst die Formel (2.3), (2.5) und (2.6)
wiedergibt. Bis auf das Quadrat eines skalaren Wertes ist das Ergebnis dieser
Transformation gleich Null, was noch zu beweisen ist.
da bekanntlich
seine Lage dadurch unverändert bleibt.
Fasst man die Formel (2.1) und (2.4) in einem Schema oder einer
Matrix zusammen, so besitzt diese eine affine Transformationseigenschaft,
die bei einer Anwendung auf sich selbst die Formel (2.3), (2.5) und (2.6)
wiedergibt. Bis auf das Quadrat eines skalaren Wertes ist das Ergebnis dieser
Transformation gleich Null, was noch zu beweisen ist.
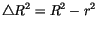 |
|
|
(2.7) |
Nun versuchen wir durch eine einfache Überlegung diese 9 Größen in ein
Schema zusammenzufassen (8 Vektoren und einen Skalar). Zuerst bilden wir aus
(1.7) und (1.10) ein orthogonales System von Vektoren, die zueinander senkrecht
stehen und fassen sie als einen komplexen Vierervektor zusammen:
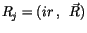 |
|
|
(2.8) |
Die Komponenten dieses Vierervektors tragen wir in einer
Matrix so ein, daß
bei einer richtigen Wahl des Vorzeichens vier linearunabhäbgige Zeilen und
vier linearunabhängige Spaltenvierervektoren entstehen. Folgende Einleitung
würde diese Auswahl erleichtern.
Zuerst ordnen wir die skalaren Komponenten in der Diagonale der Matrix
ein und so rekonstoruieren wir eine skalare Vierermatrix:
 |
|
|
(2.9) |
Nun tragen wir in der ersten Zeile die positiven Vektorkomponenten und in
der ersten Spalte ihre Spiegelbildkomponenten ein. Diese Vektoren
werden mit
polaren Vektoren bezeichnet.
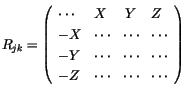 |
|
|
(2.10) |
Die restlichen Komponenten bilden die sogenannte dreidimensionalen
antisymetrische Tensor zweite Stufe, die im Grunde wie die polare Vektoren
auch aus zwei Vektoren zusammengesetzt ist. Diese Vektoren werden
axialen Vektoren genannt.
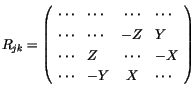 |
|
|
(2.11) |
Die Addition aus (2.9), (2.10) und (2.11) ergibt die vollständige Vierermatrix.
Sie ist antisymetrisch d.h. ihre Komponenten links der Diagonale liegend sind
das Spiegelbild der rechtsliegenden Komponenten. Sie wird als antisymetrischer
Vierertensor bezeichnet.
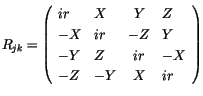 |
|
|
(2.12) |
Zum Abschluß noch ein Hinweis zur Vierertensorkoponenten: wir werden
häufiger von den Komponenten eines Vierertensors
sprechen. Damit wird immer
der erste Zeilenvierervektor der zugehörigen Matrix gemeint z.B.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ X_{1k} = ( ir \>\>, \>\>\> \vec{R} ) \>\>\>\> mit \> k = 1,2,3,4 \ $}$](IMG45.GIF) |
|
|
(2.13) |




Nächste Seite: Spiegelung der Vektoren
Aufwärts: Die Tensoren
Vorherige Seite: Die Tensoren
Inhalt
Index
root
1999-07-07

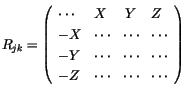
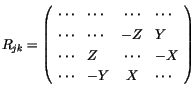
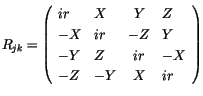
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ X_{1k} = ( ir \>\>, \>\>\> \vec{R} ) \>\>\>\> mit \> k = 1,2,3,4 \ $}$](IMG45.GIF)