




Nächste Seite: Beliebige Bezugssysteme
Aufwärts: Bezugssysteme
Vorherige Seite: Bezugssysteme
Inhalt
Index
In der dualen Physik wird die Beschreibung
der Materie unter zwei
Gesichtpunkten Impuls und Energieverhalten untersucht.
Erstens wird das Impulsverhalten eines Teilchens in
unmittelbarer Nähe seines Aufenthaltsorts untersucht. Das besitzt endliche
Abmessungen und weist ein Volumen auf (Nahbetrachtung des Teilchens).
Zweitens untersuchen wir sein Energieverhalten. Es befindet sich
weit von einem beliebigen Bezugspunkt entfernt. Folglich hat es relativ zu
dieser Entfernung vernachlässigbar
kleine Abmessungen (Fernbetrachtung des Teilchens).
Wir beschäftigen uns zuerst mit der Problematik eines Teilchens im
Fall der Nahbetrachtung. Der Raum, der das Teilchen verkörpert und es
nach außen abgrenzt wird als sein Eigenraum oder sein Volumen
bezeichnet.
Die Länge eines Maßstabs in diesem Bezugssystem ist eine reelle
Größe. In der kartesischen Koorrdinaten ist sein Ortsvektor
stets reell und hat die Komponenten:
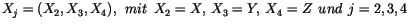 |
|
|
(1.1) |
Die Bewegung dieses Teilchens ist
gegebenenfalls eine Rotationsbewegung,
mit der es um eigenen Schwerpunkt rotiert und hier mit Eigengeschwindigkeit
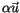 genannt wird. Die Physik, die diese Thematik abhandelt, wird mit
dem Namen Impulstheorie = IT bezeichnet.
Nun betrachten wir das Teilchen in weiter Ferne von einem Bezugspunkt
entfernt. Der Raum um ihn ist hier stets leer und der reelle Raum
verliert die Bedeutung. Hier sprechen wir von den punktförmigen Bezugssystemen.
Die Bewegung des Teilchens im leeren Raum (die Vakuum) zu unterschiedlichen
Ankunftzeiten
ist keine reelle Bahn. Seine örtliche Änderung entlang dieser Bahn nennen
wir mit der Translationsgeschwindigkeit
genannt wird. Die Physik, die diese Thematik abhandelt, wird mit
dem Namen Impulstheorie = IT bezeichnet.
Nun betrachten wir das Teilchen in weiter Ferne von einem Bezugspunkt
entfernt. Der Raum um ihn ist hier stets leer und der reelle Raum
verliert die Bedeutung. Hier sprechen wir von den punktförmigen Bezugssystemen.
Die Bewegung des Teilchens im leeren Raum (die Vakuum) zu unterschiedlichen
Ankunftzeiten
ist keine reelle Bahn. Seine örtliche Änderung entlang dieser Bahn nennen
wir mit der Translationsgeschwindigkeit 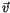 und die zugehörige
Physik hat den Namen Energietheorie = ET. Für einen
Lichtpartikel, der mit der Fortpflanzungsgeschwindigkeit c entlang
einer ähnlichen Bahn sich fortbewegt, ist die reelle Länge einer Funktion
der Zeit. Sie weist keine Richtung auf und wird als Ortsskalar
bezeichnet.
und die zugehörige
Physik hat den Namen Energietheorie = ET. Für einen
Lichtpartikel, der mit der Fortpflanzungsgeschwindigkeit c entlang
einer ähnlichen Bahn sich fortbewegt, ist die reelle Länge einer Funktion
der Zeit. Sie weist keine Richtung auf und wird als Ortsskalar
bezeichnet.
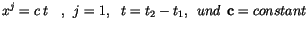 |
|
|
(1.2) |
Der Ortsvektor und der Ortskalar bilden gemeinsam die Bezugssyteme der
dualen Physik. Sie bestehen somit aus zwei Koordinatensystemen, den Einskalaren
einerseits und den Dreivektorkomponenten andererseits, die als ein komplexes
Koordinatensystem zusammengefasst wird, die zueinander Orthogonal sind.
Der Ortskalar ist zum Ortvektor Orthogonal. Mit der Orthogonalität
des kartesischen Raumes sind somit alle vier Koordinaten zueinander senkrecht. Ein
Punkt in diesem Koordinatensystem hat vier Komponenten und bildet relativ
zum Nullpunkt in diesem Fall einen Viererortsvektor.
Wir unterscheiden zwei Gruppen der Vierervektoren. Zu der ersten
Gruppe zählen wir die Vierervektoren, die zur Physik der Materie
und Antimaterie
und zu der zweiten Gruppe die Vierervektoren, die zur
makroskopischen Physik angehören.
Zu der ersten Gruppe gehören die komplexdualen Vierervektoren aus
der Impuls und Energietheorie :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ X_{j} \ = \ ( i{cT} \>, \>\> {\vec{R}} ) \>\> ; \quad
\mbox{\bf Impulstheorie \ = \ IT } \ $}$](IMG14.GIF) |
|
|
(1.3) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ x^{j} \ = \ ( \> {ct} \>, \>\> i{\vec{r}} ) \>\>\> ; \quad
\mbox{\bf Energietheorie \ = \ ET} \ $}$](IMG15.GIF) |
|
|
(1.4) |
Die reell und komplexdualen Vierervektoren bilden die zweite Gruppe, die ebenfalls
aus der Impuls - und Energietheorie bestehen:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ X^{j} \ = \ ( {cT} \>, \>\> {\vec{R}} ) \>\> ; \ \mbox{\bf Impulstheorie \ = \ IT} \ $}$](IMG16.GIF) |
|
|
(1.5) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ x_{j} \ = \ ( \> {ct} \>, \>\> i{\vec{r}} ) \>\>\> ; \ \mbox{\bf Energietheorie \ = \ ET} \ $}$](IMG17.GIF) |
|
|
(1.6) |





Nächste Seite: Beliebige Bezugssysteme
Aufwärts: Bezugssysteme
Vorherige Seite: Bezugssysteme
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ X_{j} \ = \ ( i{cT} \>, \>\> {\vec{R}} ) \>\> ; \quad
\mbox{\bf Impulstheorie \ = \ IT } \ $}$](IMG14.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ x^{j} \ = \ ( \> {ct} \>, \>\> i{\vec{r}} ) \>\>\> ; \quad
\mbox{\bf Energietheorie \ = \ ET} \ $}$](IMG15.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ X^{j} \ = \ ( {cT} \>, \>\> {\vec{R}} ) \>\> ; \ \mbox{\bf Impulstheorie \ = \ IT} \ $}$](IMG16.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\ x_{j} \ = \ ( \> {ct} \>, \>\> i{\vec{r}} ) \>\>\> ; \ \mbox{\bf Energietheorie \ = \ ET} \ $}$](IMG17.GIF)