




Nächste Seite: Das duale Wirkungsintegral
Aufwärts: Die Spiegelung der Skalaren
Vorherige Seite: Die Skalarspiegelung der Energietheorie
Inhalt
Index
Die Vierervektoren, die sich nur in ihren skalaren Komponeneten spiegeln
lassen, nennen wir die echten Axialvierervektoren. Als solchen Vektor
kann man den Hyperflächenvierervektor bezeichnen. Für seine Komponenten in
der Impulstheorie können wir schreiben :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dF_{1k} = ( \ idV \ , \ \ cdT \ d\vec{F} \ ) \ \ \ $}$](IMG178.GIF) |
|
|
(3.11) |
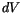 ist das Volumen und
ist das Volumen und 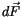 das Flächenelment der Impulstheorie.
Seine transponierte Komponente lautet :
das Flächenelment der Impulstheorie.
Seine transponierte Komponente lautet :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}( dF_{1k} )^* = ( \ -idV \ , \ \ cdT \ d\vec{F} \ ) \ \ \ $}$](IMG181.GIF) |
|
|
(3.12) |
Die Komponente des Hyperflächenvierervektors kann man aus der unteren
Beziehung
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}i\displaystyle\int \limits d\Omega_k...
... . \ J_{jk} \ = \ \displaystyle\int \limits dF_{jk} \ . \ J_{jk} \ \ \ \ \ \ $}$](IMG182.GIF) |
|
|
(3.13) |
oder
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}id\Omega_j^k \displaystyle\frac {\partial}{\partial X_{kj}}\ \ \ \ \ \ \ \ \ \ \ $}$](IMG183.GIF) |
|
|
(3.14) |
gewinnen. Der Vierervektor
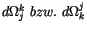 ist das
Vierervolumenelement der Impulstheorie.
Analog zu den Hyperflächenvierervektoren der Impulstheorie können wir
nun die der Energietheorie zugehörigen Gleichungen angeben.
ist das
Vierervolumenelement der Impulstheorie.
Analog zu den Hyperflächenvierervektoren der Impulstheorie können wir
nun die der Energietheorie zugehörigen Gleichungen angeben.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}df^{1k} = ( \ dv \ , \ \ icdt \ d\vec{f} \ ) \ \ \ $}$](IMG185.GIF) |
|
|
(3.15) |
Mit 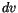 das Volumen und
das Volumen und 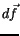 das Flächenelement der
Energietheorie lautet seine transponierte Komponente :
das Flächenelement der
Energietheorie lautet seine transponierte Komponente :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}( df^{1k} )^* = ( \ -dv \ , \ \ icdt \ d\vec{f} \ ) \ \ \ $}$](IMG188.GIF) |
|
|
(3.16) |
Analog zu IT kann man aus den Ableitungen des Vierervolumenelements
diese
Beziehungen der ET gewinnen :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}i\displaystyle\int \limits d\omega_k...
... \ \j^{jk} \ = \ \displaystyle\int \limits df^{jk} \ . \ \j^{jk} \ \ \ \ \ \ $}$](IMG189.GIF) |
|
|
(3.17) |
oder mit transponierten Komponenten
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}id\omega_j^k \displaystyle\frac {\partial}{\partial x^{kj}}\ \ \ \ \ \ \ \ \ \ $}$](IMG190.GIF) |
|
|
(3.18) |





Nächste Seite: Das duale Wirkungsintegral
Aufwärts: Die Spiegelung der Skalaren
Vorherige Seite: Die Skalarspiegelung der Energietheorie
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dF_{1k} = ( \ idV \ , \ \ cdT \ d\vec{F} \ ) \ \ \ $}$](IMG178.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}dF_{1k} = ( \ idV \ , \ \ cdT \ d\vec{F} \ ) \ \ \ $}$](IMG178.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}( dF_{1k} )^* = ( \ -idV \ , \ \ cdT \ d\vec{F} \ ) \ \ \ $}$](IMG181.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}i\displaystyle\int \limits d\Omega_k...
... . \ J_{jk} \ = \ \displaystyle\int \limits dF_{jk} \ . \ J_{jk} \ \ \ \ \ \ $}$](IMG182.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}id\Omega_j^k \displaystyle\frac {\partial}{\partial X_{kj}}\ \ \ \ \ \ \ \ \ \ \ $}$](IMG183.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}df^{1k} = ( \ dv \ , \ \ icdt \ d\vec{f} \ ) \ \ \ $}$](IMG185.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}( df^{1k} )^* = ( \ -dv \ , \ \ icdt \ d\vec{f} \ ) \ \ \ $}$](IMG188.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}i\displaystyle\int \limits d\omega_k...
... \ \j^{jk} \ = \ \displaystyle\int \limits df^{jk} \ . \ \j^{jk} \ \ \ \ \ \ $}$](IMG189.GIF)
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}id\omega_j^k \displaystyle\frac {\partial}{\partial x^{kj}}\ \ \ \ \ \ \ \ \ \ $}$](IMG190.GIF)