




Nächste Seite: Das Atom in der
Aufwärts: Das Atom
Vorherige Seite: Das Atom
Inhalt
Index
In diesem Kapitel werden wir die duale atomare Lichttheorie behandeln. In
Übereinstimmung zu den heutigen Erkenntnissen wird ein Photon dann imitiert,
falls eine spontane bzw. indizierte Energieänderung des gebundenen Teilchens
(die elektrische Ladung 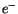 ) von einem höheren in ein tieferes
Energieniveau übergeht. Daraus resultiert, daß der mechanische
Eigen-Impuls des Teilchens
) von einem höheren in ein tieferes
Energieniveau übergeht. Daraus resultiert, daß der mechanische
Eigen-Impuls des Teilchens 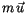 sich adäquat spontan steigert,
der aber wegen der Trägheitkraft des Teilchens für die Dauer
sich adäquat spontan steigert,
der aber wegen der Trägheitkraft des Teilchens für die Dauer 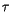 , die
sogenannte Anregungszeit verzögert in Aktion tritt.
Der Quotient aus der Teilchen-Spinenergie
, die
sogenannte Anregungszeit verzögert in Aktion tritt.
Der Quotient aus der Teilchen-Spinenergie 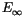 zu der Teilchen-Leistung
zu der Teilchen-Leistung
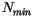 ist die genannte Anregungszeit
ist die genannte Anregungszeit 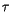 .
.
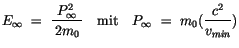 |
|
|
(11.1) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\tau \ = \ \displaystyle\frac {E_{\i...
...\mbox{mit} \quad N_{min} \ = \ e \ ({\vec{v}}_{min} . {\vec{E}}_{min}) \quad $}$](IMG821.GIF) |
|
|
(11.2) |
Berücksichtigen wir, daß
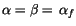 und
und
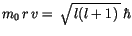 gilt, so finden wir:
gilt, so finden wir:
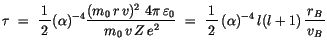 |
|
|
(11.3) |
Die Bohrsche Kreisfrequenz 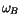 ist um Faktor
ist um Faktor 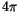 größer als die
Rydberg-Konstante
größer als die
Rydberg-Konstante 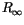 .
.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{\infty} = \displaystyle\frac {m_0 c^2\, Z^2\alpha_f^2}{2\, h\,} \quad $}$](IMG828.GIF) |
|
|
(11.4) |
Für die Anregungszeit 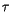 erhalten wir schließlich:
erhalten wir schließlich:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\tau \ = \ \displaystyle\frac {1}{\,...
...style\frac {\, l(l+1) \, }{Z^2}\right) \ \ 0.426649 \ \, {10}^{-8} \ s \quad $}$](IMG829.GIF) |
|
|
(11.5) |
Der Eigenenergieüberschuß führt in dieser Zeit zu starker mechanischen
Beanspruchung des Teilchens (einer Schale)
, der letztlich als Massendefekt in form eines Lichtquants emitiert wird. Die Energie dieses Lichtquants lässt sich
als Differenz zweier
Energiezustände erfassen. Folglich kann man für die freigesetzte Energie, die
Energie eines Photons schreiben:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}W \ = \ h \ \nu \quad \quad \mbox{mit} \quad \quad W = E_2 \, - \, E_1 \quad $}$](IMG830.GIF) |
|
|
(11.6) |
Photonen werden auch bei der Paarvernichtung erzeugt. Die Energiebilanz des Teilchens
und Antiteilchens lassen sich aus dem Viererimpuls der jeweiligen Theorien
ermitteln.
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_-^2 \ = \ P_0^2 \, + \, p_-^2 \quad\quad $}$](IMG831.GIF) |
|
|
(11.7) |
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_+^2 \ = \ P_0^2 \, - \, p_+^2\quad \quad $}$](IMG832.GIF) |
|
|
(11.8) |
Aus der Addition der beiden Beziehungen findet man mit
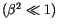 die
Energie der zwei Lichtquanten.
die
Energie der zwei Lichtquanten.
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {P_-^2}{m_0}\, + \...
...\mbox{oder} \quad \quad e^- \, + \, e^+ \, \rightarrow \, \gamma \, + \, \gamma$](IMG834.GIF) |
|
|
(11.9) |





Nächste Seite: Das Atom in der
Aufwärts: Das Atom
Vorherige Seite: Das Atom
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\tau \ = \ \displaystyle\frac {E_{\i...
...\mbox{mit} \quad N_{min} \ = \ e \ ({\vec{v}}_{min} . {\vec{E}}_{min}) \quad $}$](IMG821.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}R_{\infty} = \displaystyle\frac {m_0 c^2\, Z^2\alpha_f^2}{2\, h\,} \quad $}$](IMG828.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\tau \ = \ \displaystyle\frac {1}{\,...
...style\frac {\, l(l+1) \, }{Z^2}\right) \ \ 0.426649 \ \, {10}^{-8} \ s \quad $}$](IMG829.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}W \ = \ h \ \nu \quad \quad \mbox{mit} \quad \quad W = E_2 \, - \, E_1 \quad $}$](IMG830.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_-^2 \ = \ P_0^2 \, + \, p_-^2 \quad\quad $}$](IMG831.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}P_+^2 \ = \ P_0^2 \, - \, p_+^2\quad \quad $}$](IMG832.GIF)
![$\displaystyle \fbox{$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {P_-^2}{m_0}\, + \...
...\mbox{oder} \quad \quad e^- \, + \, e^+ \, \rightarrow \, \gamma \, + \, \gamma$](IMG834.GIF)