




Nächste Seite: Die 4. Teilchen-Gleichungen der
Aufwärts: Die 3. Teilchen-Gleichungen der
Vorherige Seite: Die 3. Teilchen-Gleichungen der
Inhalt
Index
Das Dichten-Potential
Um das Gesetz der Ladungserhaltung abzuleiten, müßen wir zuerst das Dichtenpotential
der ET ermitteln. Dazu wenden wir uns zuerst der Gleichung (7.1) zu und
schreiben für ihre rechte Seite:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i\displaystyle\int \limits_\omega \...
...int \limits_{\partial\omega} \ df^{1k} \ (\partial^{kj}\ . \
\j^{kj}) \quad $}$](IMG490.GIF) |
|
|
(7.24) |
Diese Beziehung ist der vierdimensionale Gaussche Satz. In dem linken Term
steht der Skalar 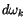 für das vierdimensionale Volumenelement. Er ist
stets imaginär und ist eine Invariante des Vierdimensionalen Bezugssystems der
ET.
Die Komponente dieses vierdimensionalen antisymetrischen Tensors7.4
für das vierdimensionale Volumenelement. Er ist
stets imaginär und ist eine Invariante des Vierdimensionalen Bezugssystems der
ET.
Die Komponente dieses vierdimensionalen antisymetrischen Tensors7.4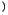 lautet :
lautet :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}d\omega_1^k \ = \ ( \ d\omega \ \ , \ \ \vec{0} \ ) \ \qquad \mbox{mit} \ \ d\omega \ = \ icdt dx dy dz \quad $}$](IMG495.GIF) |
|
|
(7.25) |
Auf der rechten Seite von (7.24) erstreckt sich das Viererintegral über die
Viererhyperfläche 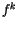 . Sie ist ein echter axialer Vierervektor der
ET.
Für seine Komponete finden wir:
. Sie ist ein echter axialer Vierervektor der
ET.
Für seine Komponete finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}df^{1k} \ = \ (\, dv \ , \ \ icdt \ d\vec{f}\, ) \qquad $}$](IMG497.GIF) |
|
|
(7.26) |
Trotz des imaginären infinitesimalen Ortsvektors 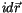 ist das dreidimensionale
Volumenelement
ist das dreidimensionale
Volumenelement 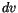 ein reeller Skalar.
Im Gegensatz zu IT ist der zweidimensionale Flächenvektor
ein reeller Skalar.
Im Gegensatz zu IT ist der zweidimensionale Flächenvektor 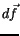 reell, aber kleiner Null.
Das bedeutet, daß die Richtung der Flächennormale
nach innen gerichtet ist.
Für die ablaufenden Prozesse in Richtung Zukunft ist der Skalar
reell, aber kleiner Null.
Das bedeutet, daß die Richtung der Flächennormale
nach innen gerichtet ist.
Für die ablaufenden Prozesse in Richtung Zukunft ist der Skalar 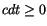 .
Aus (7.26) können wir die Viererhyperflächen-Differential ableiten:
.
Aus (7.26) können wir die Viererhyperflächen-Differential ableiten:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{\parti...
...rtial}{\partial f_y}, \ \displaystyle\frac {\partial}{\partial f_z}\, )\Big) $}$](IMG500.GIF) |
|
|
(7.27) |
Die Komponeten aus dem Produkt der runden Klammer in der linken Seite von (7.24)
lauten nun:
![$\displaystyle \fbox {$ \begin{array}{rcl}\rule[-4mm]{0cm}{1cm}R_V \left( \, (\d...
...aystyle\frac {{\vec{\j}^{\ -}}_{(ct,\vec{r})}}{c}) \right) \qquad\end{array} $}$](IMG501.GIF) |
|
|
(7.28) |
Integrieren wir die Gleichung (7.28) und berücksichtigen wir die Beziehung
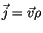 , so finden wir:
, so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\begin{array}{rcl} R_V \ \left((\, \...
...aystyle\frac {{\vec{\j}^{\ -}}_{(ct,\vec{r})}}{c}) \right) \qquad\end{array} $}$](IMG503.GIF) |
|
|
(7.29) |
Das erste Glied der skalaren Komponenten der Gleichung (7.29) stellt
das Potential
der positiven und das zweite Glied das Potential der negativen Elementarladung
( Lamb-Shift) dar. Das erste Glied der polaren Vektorkopomenten von (7.29) stellt das elektromagnetische
Vektorpotential der negativen und das zweite Glied das Vektorpotential der
positiven Elementarladung dar. Das Vektorpotential der axialen
Komponente von (7.29) ist schließlich gleich null.





Nächste Seite: Die 4. Teilchen-Gleichungen der
Aufwärts: Die 3. Teilchen-Gleichungen der
Vorherige Seite: Die 3. Teilchen-Gleichungen der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i\displaystyle\int \limits_\omega \...
...int \limits_{\partial\omega} \ df^{1k} \ (\partial^{kj}\ . \
\j^{kj}) \quad $}$](IMG490.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-i\displaystyle\int \limits_\omega \...
...int \limits_{\partial\omega} \ df^{1k} \ (\partial^{kj}\ . \
\j^{kj}) \quad $}$](IMG490.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}d\omega_1^k \ = \ ( \ d\omega \ \ , \ \ \vec{0} \ ) \ \qquad \mbox{mit} \ \ d\omega \ = \ icdt dx dy dz \quad $}$](IMG495.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}df^{1k} \ = \ (\, dv \ , \ \ icdt \ d\vec{f}\, ) \qquad $}$](IMG497.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\displaystyle\frac {\partial}{\parti...
...rtial}{\partial f_y}, \ \displaystyle\frac {\partial}{\partial f_z}\, )\Big) $}$](IMG500.GIF)
![$\displaystyle \fbox {$ \begin{array}{rcl}\rule[-4mm]{0cm}{1cm}R_V \left( \, (\d...
...aystyle\frac {{\vec{\j}^{\ -}}_{(ct,\vec{r})}}{c}) \right) \qquad\end{array} $}$](IMG501.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}\begin{array}{rcl} R_V \ \left((\, \...
...aystyle\frac {{\vec{\j}^{\ -}}_{(ct,\vec{r})}}{c}) \right) \qquad\end{array} $}$](IMG503.GIF)