



Nächste Seite: Die Wirkung in allgemeinen
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Die Wirkung in der
Inhalt
Index
Analog zu IT variieren wir die Integralgleichungen (4.46) und (4.47).
Zuerst beschäftigen wir
uns mit der rechten Seite von (4.46) und variieren zunächst die zeitabhängige
Bahn. Die festen Anfangs und Endpunkte bleiben unvariiert :
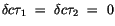
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ m_0 c \displaystyle\...
...au_1}^{c\tau_2} \delta (cdt \sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}) \ $}$](IMG299.GIF) |
|
|
(4.54) |
Analog zu IT geben wir die Beziehungen bekannt, die wir bei der Variation
einsetzen.
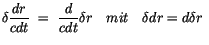 |
|
|
(4.55) |
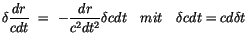 |
|
|
(4.56) |
Unter der Berücksichtigung der linken Seite (4.56) erhalten wir für den
Integrand:
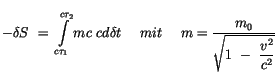 |
|
|
(4.57) |
Analog zu IT finden wir durch die partielle Integration :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ mc \ c\delta t {\lef...
...tau_1}^{c\tau_2} \ (\displaystyle\frac {d}{ds} mc \ c\delta t ) \ ds \ = \ 0 $}$](IMG303.GIF) |
|
|
(4.58) |
Wegen
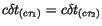 ist das erste Glied dieser
Beziehung gleich null.
Wegen dem linken Teil von (4.54) muß das zweite Glied ebenfalls verschwinden.
Diese Bedingung tritt dann ein, falls der Integrand verschwindet. Daraus können
wir auf die Konstanz der Vierergeschwindigkeit schließen.
Das bedeutet aber nicht, daß ein freies Teilchen, daß keinen äußeren
Einflüssen unterliegt, und keine elektromagnetischen Signale empfängt oder aussendet,
ruhen muß. Die Konstante Geschwindigkeit, mit der sich das Teilchen fortbewegt,
ist gleichzeitig die Bewegung seines Bezugssystems.
Analog kann man hier den Ortsvektor
ist das erste Glied dieser
Beziehung gleich null.
Wegen dem linken Teil von (4.54) muß das zweite Glied ebenfalls verschwinden.
Diese Bedingung tritt dann ein, falls der Integrand verschwindet. Daraus können
wir auf die Konstanz der Vierergeschwindigkeit schließen.
Das bedeutet aber nicht, daß ein freies Teilchen, daß keinen äußeren
Einflüssen unterliegt, und keine elektromagnetischen Signale empfängt oder aussendet,
ruhen muß. Die Konstante Geschwindigkeit, mit der sich das Teilchen fortbewegt,
ist gleichzeitig die Bewegung seines Bezugssystems.
Analog kann man hier den Ortsvektor 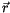 in (4.48) variieren. unter der Berücksichtigung von
(4.55) erhalten wir für die gleiche Beziehung:
in (4.48) variieren. unter der Berücksichtigung von
(4.55) erhalten wir für die gleiche Beziehung:
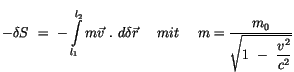 |
|
|
(4.59) |
Nach partieller Integration finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = -\ m \vec{v} \ . \ \de...
... (\displaystyle\frac {d}{ds} m \vec{v} \ . \ \delta \vec{r} ) \ ds \ = \ 0 \ $}$](IMG306.GIF) |
|
|
(4.60) |
Zu dem gleichen Ergebnis gelänge man, analog zu der IT, falls man die
Gleichung (4.46) variiert:
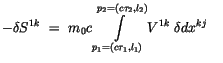 |
|
|
(4.61) |
integrieren wir diese Gleichung partial, so finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S^{1k} \ = \ P^{1k} \ . \ \d...
...2} \ (\displaystyle\frac {d}{ds} P^{1k} \ . \ \delta x^{kj} ) \ ds \ = \ 0 \ $}$](IMG308.GIF) |
|
|
(4.62) |
Dieses Ergebnis stimmt mit den Gleichungen (4.58) und (4.60) überein.
Der erste Term dieser Gleichung ist der Drehimpuls 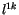 . Eine andere
Darstellung dieser Gleichung lautet:
. Eine andere
Darstellung dieser Gleichung lautet:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-l^{1k} \ = \ x^{1k} \ . \ p^{kj} \quad \quad $}$](IMG310.GIF) |
|
|
(4.63) |
Für seine Komponente finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-l^{1k} \ = \ \left( (\, x^{1k} . p^...
..., ) \ , \ x^{1k} \times (\, p^{2j}\, , p^{3j}\, , p^{4j}\, )\, \right) \quad $}$](IMG311.GIF) |
|
|
(4.64) |
Berücksichtigen wir
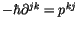 , so erhalten wir für die Gleichung
(4.63):
, so erhalten wir für die Gleichung
(4.63):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}l^{1k} \ = \ x^{1k} \ . \ \hbar \partial^{jk}\quad \quad $\ }$](IMG313.GIF) |
|
|
(4.65) |
deren Komponenten lauten:
und nach Errechnung des skalaren Terms finden wir für 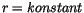 :
:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}l^{1k} \ = \ \left( \, \hbar \ , \ i...
... grad} \, ct \, + \, \hbar (\, \vec{r} \times {\sf grad}\, )\, \right) \quad $}$](IMG316.GIF) |
|
|
(4.66) |
Der letzte Term in der runden Klammer ist der axiale Drehimpulsvektor
( Drehmoment). Das Quadrat dieses Vektorproduktes ist gleich:
Das letztere Glied ist auch bei nichtkonstantem Radiusvektor eine
Konstante und trägt nur zur Nullpunktverschiebung bei, so daß schließlich
das Drehimpulsquadrat der Lösung der Differentialgleichung
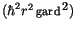 gleichkommt.
In den kommenden Kapiteln werden wir dieser Differentialgleichungen in Polarkoordinaten
begegnen und deren Eigenwerte errechnen. Analog zu IT finden wir vor:
gleichkommt.
In den kommenden Kapiteln werden wir dieser Differentialgleichungen in Polarkoordinaten
begegnen und deren Eigenwerte errechnen. Analog zu IT finden wir vor:




Nächste Seite: Die Wirkung in allgemeinen
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Die Wirkung in der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ m_0 c \displaystyle\...
...au_1}^{c\tau_2} \delta (cdt \sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}) \ $}$](IMG299.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ m_0 c \displaystyle\...
...au_1}^{c\tau_2} \delta (cdt \sqrt{ 1 \ - \ \displaystyle\frac {v^2}{c^2}}) \ $}$](IMG299.GIF)
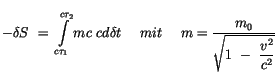
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ mc \ c\delta t {\lef...
...tau_1}^{c\tau_2} \ (\displaystyle\frac {d}{ds} mc \ c\delta t ) \ ds \ = \ 0 $}$](IMG303.GIF)
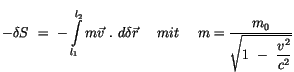
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = -\ m \vec{v} \ . \ \de...
... (\displaystyle\frac {d}{ds} m \vec{v} \ . \ \delta \vec{r} ) \ ds \ = \ 0 \ $}$](IMG306.GIF)
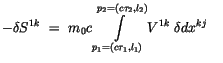
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S^{1k} \ = \ P^{1k} \ . \ \d...
...2} \ (\displaystyle\frac {d}{ds} P^{1k} \ . \ \delta x^{kj} ) \ ds \ = \ 0 \ $}$](IMG308.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-l^{1k} \ = \ x^{1k} \ . \ p^{kj} \quad \quad $}$](IMG310.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-l^{1k} \ = \ \left( (\, x^{1k} . p^...
..., ) \ , \ x^{1k} \times (\, p^{2j}\, , p^{3j}\, , p^{4j}\, )\, \right) \quad $}$](IMG311.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}l^{1k} \ = \ x^{1k} \ . \ \hbar \partial^{jk}\quad \quad $\ }$](IMG313.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}l^{1k} \ = \ \hbar \left( \, ( \, \d...
...}\vec{r}\, ) \, + \, \hbar (\, \vec{r} \times {\sf grad}\, )\, \right) \quad $}$](IMG314.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}l^{1k} \ = \ \left( \, \hbar \ , \ i...
... grad} \, ct \, + \, \hbar (\, \vec{r} \times {\sf grad}\, )\, \right) \quad $}$](IMG316.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L \, = \, \hbar \, \sqrt{l\, (\, l + 1 \, )} \quad \quad $}\quad \quad \mbox{mit} \quad l\, = \, 0, 1, 2, . . .$](IMG319.GIF)