




Nächste Seite: Der Viererimpuls der Energietheorie
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Die Wirkung in der
Inhalt
Index
Das Prinzip der kleinsten Wirkung, von dem wir schon flüchtig gesprochen
haben, basiert
auf Variation der Integralgleichungen (4.10) und (4.11). Zuerst beschäftigen wir
uns mit der rechten Seite von (4.11) und variieren zunächst die zeitunabhängige
Bahn. Die Bahnstücke, die durch zwei feste Punkte gehen, sollen an diesem
unvariiert bleiben. Es soll also gelten:
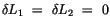
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ m_0 c \displaystyle\...
...mits_{L_1}^{L_2} \delta (dR \sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}) \ $}$](IMG242.GIF) |
|
|
(4.22) |
Bevor wir die Variation durchführen, verweisen wir auf einige Beziehungen,
die wir bei den Berechnungen einsetzen. Darin sind auch zeitabhängige Formeln
enthalten, die wir an dieser Stelle nicht anwenden.
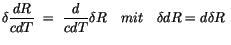 |
|
|
(4.23) |
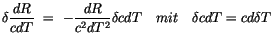 |
|
|
(4.24) |
Unter der Berücksichtigung der linken Seite (4.23) finden wir für den
Integrand:
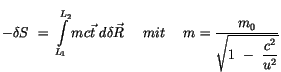 |
|
|
(4.25) |
Durch die partielle Integration erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ mc \vec{t} \ . \ \de...
... \ (\displaystyle\frac {d}{ds} mc \vec{t} \ .\ \delta \vec{R} ) \ ds \ = \ 0 $}$](IMG246.GIF) |
|
|
(4.26) |
Das erste Glied dieser Gleichung ist wegen
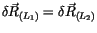 gleich null. Das
zweite Glied muß ebenfalls verschwinden, damit wir dem linken Teil von (4.22)
gerecht werden. Diese Bedingung ist dann erfüllt, falls der Integrand gleich null
ist. Daraus können wir auf die Konstanz der Vierergeschwindigkeit schließen.
Das bedeutet aber keineswegs, daß ein freies Teilchen, daß keinen äußeren
Einflüssen unterliegt, und keine elektromagnetischen Signale empfängt oder aussendet,
ruhen muß. Die Konstante Geschwindigkeit
gleich null. Das
zweite Glied muß ebenfalls verschwinden, damit wir dem linken Teil von (4.22)
gerecht werden. Diese Bedingung ist dann erfüllt, falls der Integrand gleich null
ist. Daraus können wir auf die Konstanz der Vierergeschwindigkeit schließen.
Das bedeutet aber keineswegs, daß ein freies Teilchen, daß keinen äußeren
Einflüssen unterliegt, und keine elektromagnetischen Signale empfängt oder aussendet,
ruhen muß. Die Konstante Geschwindigkeit 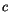 ist zugleich die Bewegung seines Bezugssystems.
Analog kann man in (4.22) die Zeit variieren. Unter der Berücksichtigung von
(4.24) erhalten wir für die gleiche Beziehung :
ist zugleich die Bewegung seines Bezugssystems.
Analog kann man in (4.22) die Zeit variieren. Unter der Berücksichtigung von
(4.24) erhalten wir für die gleiche Beziehung :
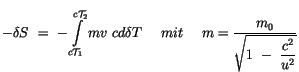 |
|
|
(4.27) |
integrieren wir diese Gleichung partial, so finden wir :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = -\ mv \ c\delta T {\le...
...^{c{\cal T}_2} \ (\displaystyle\frac {d}{ds} mv \ c\delta T ) \ ds \ = \ 0 \ $}$](IMG250.GIF) |
|
|
(4.28) |
Zu dem gleichen Ergebnis gelangt man, falls man die Gleichung (4.10) variiert:
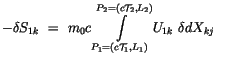 |
|
|
(4.29) |
integrieren wir diese Beziehung partial, so finden wir übereinstimmend mit (4.26) und
(4.28):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S_{1k} \ = \ P_{1k} \ . \ \d...
...2} \ (\displaystyle\frac {d}{ds} P_{1k} \ . \ \delta X_{kj} ) \ ds \ = \ 0 \ $}$](IMG252.GIF) |
|
|
(4.30) |
Der erste Term dieser Gleichung ist der Eigendrehimpuls 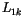 . Eine andere
Darstellung dieser Gleichung lautet:
. Eine andere
Darstellung dieser Gleichung lautet:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ X_{1k} \ . \ P_{kj} \quad \quad $}$](IMG254.GIF) |
|
|
(4.31) |
Für seine Komponente finden wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ \left( (\, X_{1k} . P_{1j}\, ) \ , \ X_{1k} \times (\, P_{2j}\, , P_{3j}\, , P_{4j}\, )\,\right) \quad $}$](IMG255.GIF) |
|
|
(4.32) |
Berücksichtigen wir
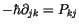 , so erhalten wir für die Gleichung
(4.31):
, so erhalten wir für die Gleichung
(4.31):
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = -\ X_{1k} \ . \ \hbar \partial_{jk}\quad \quad $}$](IMG257.GIF) |
|
|
(4.33) |
deren Komponenten lauten:
und nach Ausrechnung des skalaren Terms und beim konstanten Radius-Vektor
erhalten wir:
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ \left(\, \hbar\, \ , \ ...
...grad} \, cT \, + \, \hbar (\, \vec{R} \times {\bf grad}\, ) \, \right) \quad $}$](IMG259.GIF) |
|
|
(4.34) |
Der letzte Term in der runden Klammer ist der axiale Drehimpulsvektor
( Eigen-Drehmoment). Das Quadrat dieses Vektorproduktes ist gleich:
Bei konstantem Radiusvektor
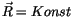 verschwindet der letzte Term,
so daß schließlich
das Drehimpulsquadrat die Lösung der Differentialgleichung
verschwindet der letzte Term,
so daß schließlich
das Drehimpulsquadrat die Lösung der Differentialgleichung
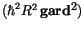 gleichkommt.
Die Eigenwerte dieser Differentialgleichung werden wir in den kommenden Kapiteln
begegnen und deren Lösungen kennenlernen. man findet vor:
gleichkommt.
Die Eigenwerte dieser Differentialgleichung werden wir in den kommenden Kapiteln
begegnen und deren Lösungen kennenlernen. man findet vor:





Nächste Seite: Der Viererimpuls der Energietheorie
Aufwärts: Das Prinzip der kleinsten
Vorherige Seite: Die Wirkung in der
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ m_0 c \displaystyle\...
...mits_{L_1}^{L_2} \delta (dR \sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}) \ $}$](IMG242.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ m_0 c \displaystyle\...
...mits_{L_1}^{L_2} \delta (dR \sqrt{ 1 \ - \ \displaystyle\frac {c^2}{u^2}}) \ $}$](IMG242.GIF)
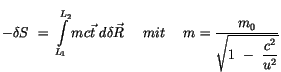
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = \ mc \vec{t} \ . \ \de...
... \ (\displaystyle\frac {d}{ds} mc \vec{t} \ .\ \delta \vec{R} ) \ ds \ = \ 0 $}$](IMG246.GIF)
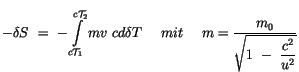
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S \ = -\ mv \ c\delta T {\le...
...^{c{\cal T}_2} \ (\displaystyle\frac {d}{ds} mv \ c\delta T ) \ ds \ = \ 0 \ $}$](IMG250.GIF)
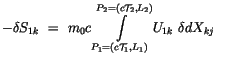
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}-\delta S_{1k} \ = \ P_{1k} \ . \ \d...
...2} \ (\displaystyle\frac {d}{ds} P_{1k} \ . \ \delta X_{kj} ) \ ds \ = \ 0 \ $}$](IMG252.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ X_{1k} \ . \ P_{kj} \quad \quad $}$](IMG254.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ \left( (\, X_{1k} . P_{1j}\, ) \ , \ X_{1k} \times (\, P_{2j}\, , P_{3j}\, , P_{4j}\, )\,\right) \quad $}$](IMG255.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = -\ X_{1k} \ . \ \hbar \partial_{jk}\quad \quad $}$](IMG257.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ \hbar \left(\, (\, \dis...
...ial T}\vec{R}\, ) \, + \, (\, \vec{R} \times {\bf grad}\, ) \, \right) \quad $}$](IMG258.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}L_{1k} \ = \ \left(\, \hbar\, \ , \ ...
...grad} \, cT \, + \, \hbar (\, \vec{R} \times {\bf grad}\, ) \, \right) \quad $}$](IMG259.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}j \, = \, \hbar \, (\, l \, + \, s \...
...= 0, 1, 2, . . \quad \mbox{und} \quad s\, = \pm\displaystyle\frac {1}{\, 2 \, }$](IMG263.GIF)