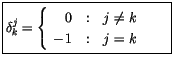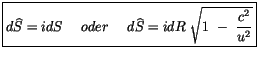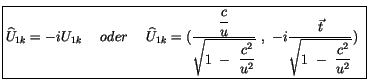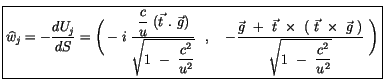Nächste Seite: Die Skalarspiegelung der Energietheorie
Aufwärts: Tensormultiplikation unter den skalaren
Vorherige Seite: Tensormultiplikation unter den skalaren
Inhalt
Index
In der Impulstheorie ist das Tensorprodukt unter den Skalarenspiegelung
durch die Beziehungen :
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(dX_{jk}) \ . \ (dX_{jk})^* = (dX_j)...
...ta}^j_k \ \ \ \ \ \ \ mit \ \ (dX_{jk})^* = {\delta}^j_k \ \ dX_{kj} \ \ \ \ $}$](IMG161.GIF) |
|
|
(3.1) |
gegeben. Die transponierte Matrix wird durch (* - Zeichen) von der Normalform
unterschieden. Der Einheitstensor der Skalarspiegelung auf der rechten Seite
von (3.1) unterscheidet sich von dem Einheitstensor der Vektorspiegelung
(2.22) durch das negative Vorzeichen.
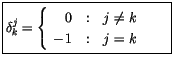 |
|
|
(3.2) |
Das hat zur Folge, daß die Komponentenbeträge dieser Vierertensoren imaginänrer
Natur sind. Erwähnenswert bleibt der Abstand, der nicht mehr reell ist. Dieser
neue Skalar verändert die Komponenten der Vierergeschwindigkeiten, die bis
auf den Faktor 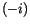 der Vierergeschwindigkeit den Vektorspiegelungen
gleichkommt. Ihre Viererbeschleunigungen dagegen stimmen bis auf den Faktor
der Vierergeschwindigkeit den Vektorspiegelungen
gleichkommt. Ihre Viererbeschleunigungen dagegen stimmen bis auf den Faktor
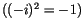 überein. Mit
überein. Mit 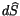 bezeichnen wir den Abstand und
erhalten :
bezeichnen wir den Abstand und
erhalten :
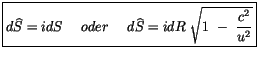 |
|
|
(3.3) |
Für die Vierergeschwindigkeit
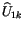 können wir schreiben :
können wir schreiben :
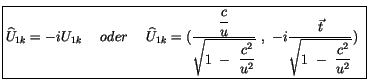 |
|
|
(3.4) |
und schließlich lautet der Viererbeschleunigungsvektor 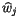 :
:
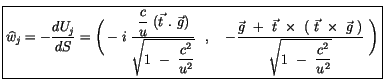 |
|
|
(3.5) |





Nächste Seite: Die Skalarspiegelung der Energietheorie
Aufwärts: Tensormultiplikation unter den skalaren
Vorherige Seite: Tensormultiplikation unter den skalaren
Inhalt
Index
root
1999-07-07
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(dX_{jk}) \ . \ (dX_{jk})^* = (dX_j)...
...ta}^j_k \ \ \ \ \ \ \ mit \ \ (dX_{jk})^* = {\delta}^j_k \ \ dX_{kj} \ \ \ \ $}$](IMG161.GIF)
![$\displaystyle \fbox {$\rule[-4mm]{0cm}{1cm}(dX_{jk}) \ . \ (dX_{jk})^* = (dX_j)...
...ta}^j_k \ \ \ \ \ \ \ mit \ \ (dX_{jk})^* = {\delta}^j_k \ \ dX_{kj} \ \ \ \ $}$](IMG161.GIF)